CS231n笔记01：kNN分类与线性分类

P1：kNN与距离函数

k最近邻分类器

kNN(k-Nearest Neighbor)分类器，就是对于每一张测试集中的图片，找到与它最接近的k张图片，从这k张图片中选出最多的一个种类作为它的的种类。

放到这张图上来说就是将训练集抽象成不同颜色（代表不同种类）的数据点，整个空间就是可能出现的数据点的集合，kNN分类器使用训练集中的数据点来划分这个空间，测试集中的点落在哪一个区域内就归为哪一类。图中的灰色区域则是出现“平票”的区域。

距离函数

对比两张图片之间的距离时，将W*H的图片（每个像素为一个3维向量）拉伸成W*H*3的向量，然后计算这两个向量之间的距离。有以下两种计算距离的函数：

L1 距离：向量各个维度上差的绝对值之和，对单个大差异的惩罚是线性的，因此更不容易被单个异常值主导。
L2 距离：向量各个维度上差的平方和开根号，平方项会放大大差异的影响。当把图像看作像素向量时，若两张图像在少数像素上有巨大差异（例如一个噪点或遮挡），L2 会把这类差异放大，导致距离很大；而 L1 会把这些差异按绝对值线性累加，对整体相似性影响较小。

交叉验证

将模型用于测试集之前需要选取一些参数（如k值，距离函数等），这些参数不能直接从训练数据中得到，称为超参数（Hyperparameters）。可以将训练数据分为训练集和验证集（Validation sets），针对不同的超参数进行训练与评估，作为超参数选择的依据。这个过程可以避免将测试集直接当作调参的对象，减少过拟合测试集的风险。

# assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
# recall Xtr_rows is 50,000 x 3072 matrix
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
Ytr = Ytr[1000:]

# find hyperparameters that work best on the validation set
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:

  # use a particular value of k and evaluation on validation data
  nn = NearestNeighbor()
  nn.train(Xtr_rows, Ytr)
  # here we assume a modified NearestNeighbor class that can take a k as input
  Yval_predict = nn.predict(Xval_rows, k = k)
  acc = np.mean(Yval_predict == Yval)
  print 'accuracy: %f' % (acc,)

  # keep track of what works on the validation set
  validation_accuracies.append((k, acc))

在CIFAR-10这个例子中，在不同的k值下，将前1000个数据作为验证集，后49000个作为训练集进行训练和验证，得到最终的准确度。这段代码可以给出用于测试集最合适的超参数k。

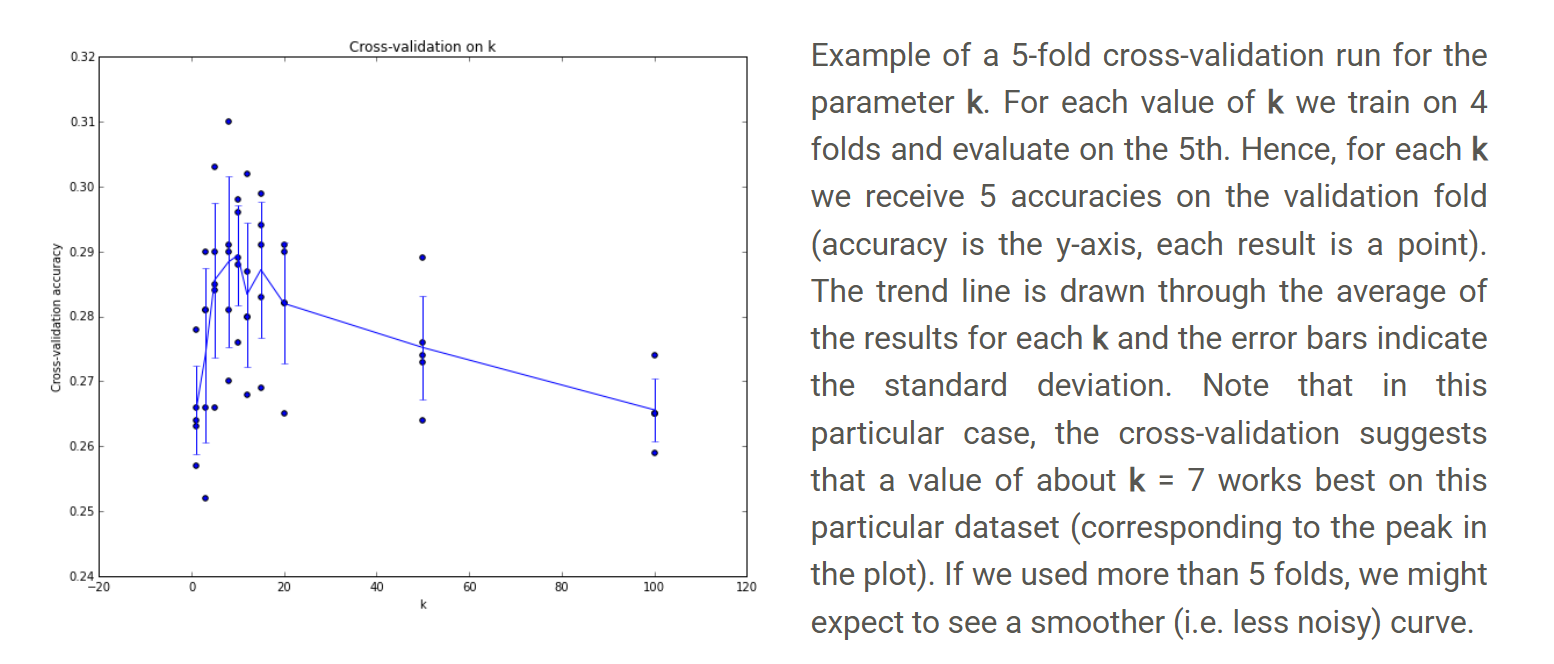
为了减小训练和验证过程中的噪声,可以使用不同的训练集和验证集划分来得到更加稳定的性能估计，即交叉验证。比较常用的方法是k折交叉验证：将训练集分成k份，每次选取1份作为验证集，其余k-1份作为训练集，最后计算k次准确值的平均值用于评估准确性。

P2：线性分类器

将每一张图片当作一个向量 $x_i$ ，其维度 $D = 3WH$ 。再给定 $K$ 个分类，我们的问题就变成了将一个D维的向量映射到K维的分类向量上。使用一个矩阵运算就可以达到这种效果：
$f(x_i,W,b)=Wx_i+b$
其中W为K*D矩阵，x为D*1向量，b为K*1向量。计算出来的向量代表一张图片在各个分类上的评分，如下图所示：

W的每一个行向量将x的每一个维度线性组合得到一个分数，用这个分数来衡量图片更接近哪一个类别。对x各个维度的线性组合，在二维空间中是一条线，在三维空间中则是一个平面，将这个线性变换放到一个二维空间上可以更加直观地理解线性分类器的工作方式：

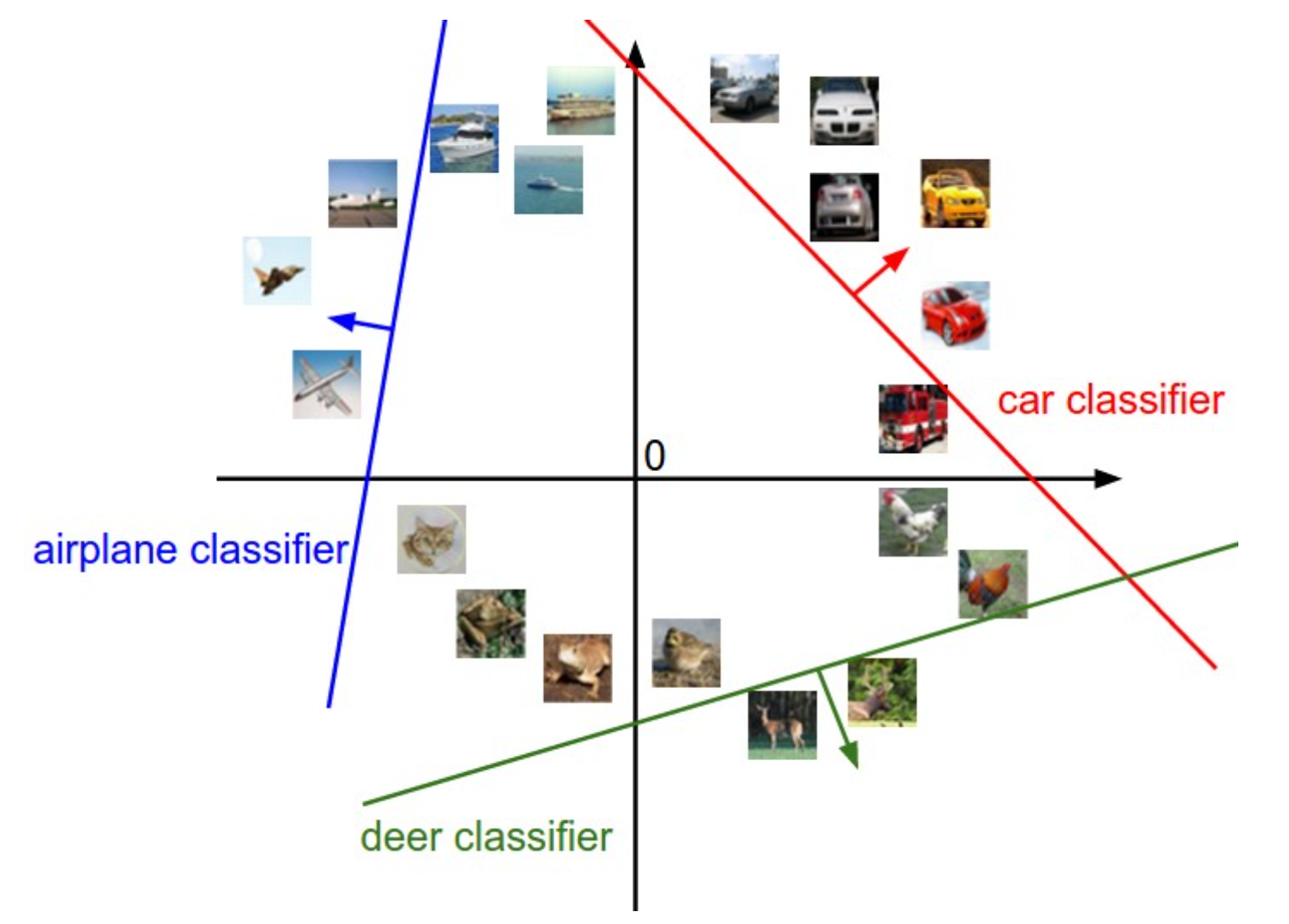
在二维空间中每一个 $w_1x+w_2y=0$ 都是一条直线，K个这样的直线将空间分割成若干区域，可以根据图像（在这里是数据点）相对于每条直线的位置判断其种类。
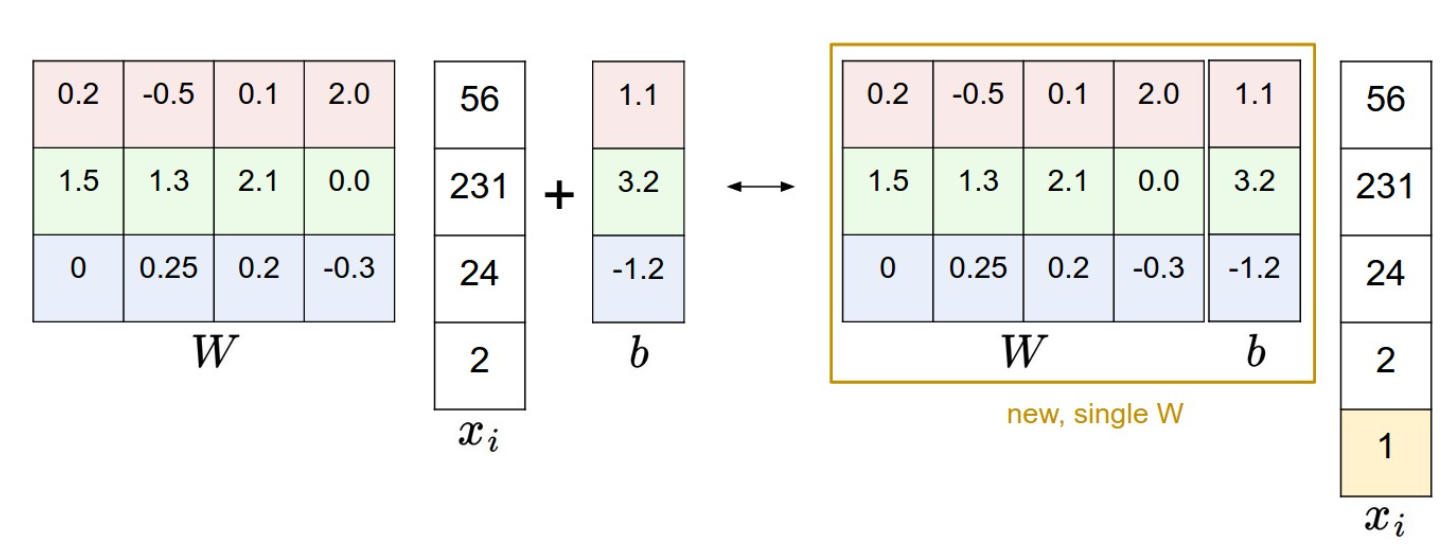
还有一个把 $f$ 变成一次矩阵乘的Trick：