计算机视觉-02：损失函数

对第 $i$ 个样本，输入 $x_i$，模型输出分数向量 $s=f(x_i;W)\in\mathbb{R}^C$，其中 $s_j$ 表示该样本在第 $j$ 类上的分数。直觉上，预测准确则 loss 低，预测错误则 loss 高。

损失函数最常见的两种选择有 Hinge loss 和 Softmax loss。

Hinge loss

多分类 SVM 希望：正确类的分数 $s_{y_i}$ 比每个错误类分数 $s_j$ 至少高一个固定间隔（margin）$\Delta$。

这里的分数 $s_j$ 不是概率，而是线性分类器给出的相对偏好。Hinge loss 的关注点也不是“正确类概率是多少”，而是“正确类有没有比所有错误类高出足够安全距离”。因此只要 margin 已经满足，它就不会继续奖励更大的分数差距；如果某个错误类离正确类太近，就会按差距线性惩罚。

对单个样本的 loss 定义为：

$$L_i = \sum_{j\neq y_i} \max\big(0,\; s_j - s_{y_i} + \Delta\big)$$

若 $s_{y_i} \ge s_j + \Delta$，这一项为 0（该错误类“达标了”）
若 $s_{y_i} < s_j + \Delta$，就按“差多少”线性惩罚

在二分类里经常把标签写成 $y\in\{-1,+1\}$，预测打分为 $t$（例如 $t=w^Tx$），hinge loss 常写成：

$$\ell(t,y)=\max(0, 1-y\,t)$$

直观对应关系：分类正确且“置信度/间隔”足够大（$y\,t\ge 1$）时，loss 为 $0$；分类错或置信度不够（$y\,t<1$）时，进行线性惩罚。

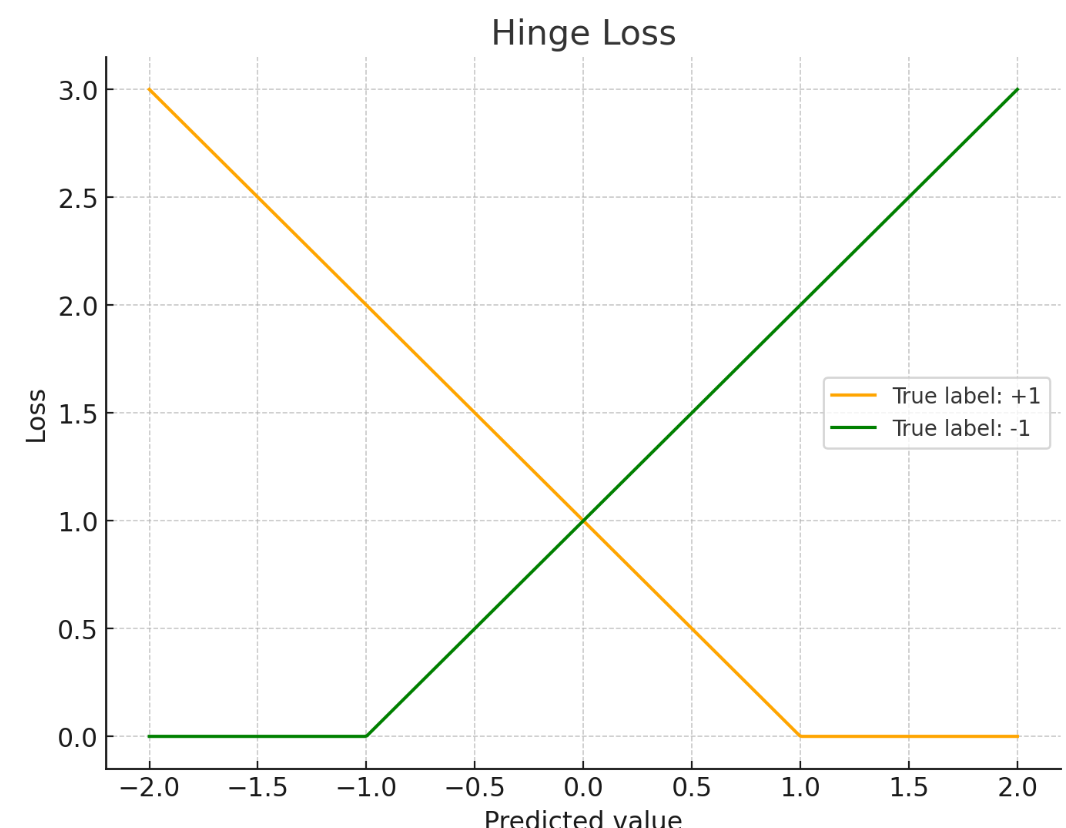
一些实现里还会用 $\mathrm{squaredHinge}=\max(0,1-y t)^2$，对违反 margin 的样本惩罚更重。

Softmax loss

Softmax 把分数当作未归一化的对数概率（logits），并得到类别概率：

与 Hinge loss 相比，Softmax loss 会把所有类别分数一起放进一个概率分布中解释。正确类分数升高会提高 $p_{y_i}$，错误类分数升高则会通过分母压低正确类概率。因此它不仅关心正确类和单个错误类之间的 margin，也关心整个分数向量的相对形状。

$$p_j = \frac{e^{s_j}}{\sum_k e^{s_k}}$$

直观来看是这样：先使用指数将得到的分数全部变为正数，再归一化为概率分布。将交叉熵作为损失，将 softmax 代入 $L=-\log P$ 即可得到第 $i$ 项的损失函数。

$$L_i = -\log\left(\frac{e^{s_{y_i}}}{\sum_j e^{s_j}}\right) = -s_{y_i} + \log\sum_j e^{s_j}$$

softmax 里有指数，$e^{s_j}$ 可能非常大导致溢出。常用的稳定技巧：

$$s \leftarrow s - \max_j s_j$$

因为对所有分数加同一个常数不会改变 softmax 的结果（分子分母同乘一个常数会约掉），但能显著提升数值稳定性。

Hinge vs Softmax

两者在实践中都很常见，效果通常接近，但优化“性格”不同：

1. Hinge / SVM 更“局部”：只关心是否超过 margin；一旦满足就不再推动分数继续分离
2. Softmax 更“全局”：永远不会完全满意，总想让正确类概率更大、错误类更小

一个对比：

对于分数 $[10,-100,-100]$ 和 $[10,9,9]$，只要 margin 满足，SVM 可能都给 0 loss；Softmax 会认为 $[10,9,9]$ “不够自信”，因为错误类也很接近，会产生更大 loss。

信息论补充——熵和交叉熵

这一部分的目标是解释为什么分类里常把损失写成 $-\log P$。从信息论角度看，概率越低的事件越“意外”，需要付出的编码代价越高；训练分类器时，让模型给正确类别更高概率，就等价于降低真实标签在模型分布下的编码代价。

因此 Softmax loss 不只是一个经验公式，它可以同时从概率最大似然和信息编码两个角度理解。

自信息（Surprisal）与编码长度

信息论把一个事件 $x$ 发生时携带的信息量定义为自信息：

$$I(x) = -\log p(x)$$

它可以理解为：如果你用概率 $p(x)$ 来做无损编码，那么事件越罕见（$p(x)$ 越小），所需编码长度越长。

备注：对数底为 2 时单位是 bit；用自然对数时单位是 nat。深度学习里默认用自然对数更常见。

熵（Entropy）= 最小平均编码长度

若随机变量服从真实分布 $P$，熵定义为“平均意义下的最小编码长度”（香农的核心观点）：

$$H(P) = \mathbb{E}_{x\sim P}[-\log P(x)] = -\sum_x P(x)\log P(x)$$

直觉：分布越“平均”（不确定性越大），熵越大；若几乎总发生同一件事，熵就很小。

交叉熵（Cross-Entropy）= 用 Q 去编码来自 P 的数据

现实里我们通常不知道真实分布 $P$，模型给出一个估计分布 $Q$。

如果你用 $Q$ 来编码来自 $P$ 的样本，平均编码长度就是交叉熵：

$$H(P,Q)=\mathbb{E}_{x\sim P}[-\log Q(x)] = -\sum_x P(x)\log Q(x)$$

交叉熵与熵的关键关系：

$$H(P,Q)=H(P)+D_{KL}(P\|Q)\;\ge\;H(P)$$

因为 KL 散度 $D_{KL}\ge 0$，所以用“错误的分布” $Q$ 编码，平均长度只会更长；只有当 $Q=P$ 时才达到最短。

为什么 Softmax loss 就是交叉熵

分类任务里，标签通常是 one-hot：真实分布 $P$ 把全部概率质量放在正确类别 $y$ 上（$P(y)=1$，其余为 0）。

这时：

• $H(P)=0$（因为它完全确定）
• 交叉熵退化为

$$H(P,Q) = -\log Q(y)$$

而 $Q(y)$ 正是 softmax 输出的正确类概率 $p_{y}$，因此 Softmax 的交叉熵损失就是：

$$L_i = -\log p_{y_i}$$

二分类交叉熵（BCE）常用形式

若二分类标签 $y\in\{0,1\}$，模型预测正类概率为 $p$，则

$$\mathrm{BCE}(y,p)= -\big[y\log p + (1-y)\log(1-p)\big]$$

它同样是“真实分布（由标签给出）”与“模型分布”的交叉熵。

当 $y=1$ 时，BCE 只剩下 $-\log p$，模型越确信正类，损失越小；当 $y=0$ 时，BCE 只剩下 $-\log(1-p)$，模型越确信负类，损失越小。多分类 Softmax loss 可以看作同一思想在多个互斥类别上的推广。

最小化负对数似然

课上直接写 $L=-\log P$。当时没看懂，在《Understanding Deep Learning》里找到一段对数似然的证明：

假设数据独立同分布，训练集的条件似然可写成乘积

$$\Pr(y_1,\dots,y_I\mid x_1,\dots,x_I)=\prod_{i=1}^{I}\Pr(y_i\mid x_i)$$

于是最大似然准则是最大化联合概率（似然）：

$$\hat\phi = \arg\max_{\phi} \prod_{i=1}^{I} \Pr\big(y_i\mid f(x_i,\phi)\big)$$

为避免小概率连乘带来的数值下溢问题，对似然取对数；由于 $\log$ 单调递增，最优点不变：

$$\hat\phi =\arg\max_{\phi}\log\prod_{i=1}^{I}\Pr\big(y_i\mid f(x_i,\phi)\big) =\arg\max_{\phi}\sum_{i=1}^{I}\log\Pr\big(y_i\mid f(x_i,\phi)\big)$$

把“最大化似然”改写成“最小化损失”，就得到负对数似然：

$$\hat\phi =\arg\min_{\phi}\left[-\sum_{i=1}^{I}\log\Pr\big(y_i\mid f(x_i,\phi)\big)\right] \equiv \arg\min_{\phi} L(\phi)$$

当使用 softmax 时，$\Pr(y_i\mid f(x_i,\phi))$ 就是正确类的 softmax 概率。