CS231n笔记03：正则化

假设我们已经找到一组参数 $W$ ，能把训练集每个样本都分对，并且对所有错误类都满足 margin（于是对所有样本 $L_i=0$ ）。这组 $W$ 通常不是唯一的。因为只要 $W$ 满足 margin，那么对任意 $\lambda>1$ ， $\lambda W$ 也同样满足：

分数 $f(x;W)$ 会整体按比例变大
正确类与错误类之间的分数差也按比例变大
hinge loss 只关心“有没有超过间隔”，一旦超过就变 0
所以“数据损失=0”并不能表达我们对参数的偏好，会出现一堆“同样正确、但尺度不同”的解。

P1：正则化

解决办法是在目标函数里加入仅依赖参数的惩罚项 $R(W)$ ，用来编码“更偏好哪类权重”。最常见的是L2正则（岭回归）：

$R(W)=\sum_k\sum_l W_{k,l}^2$

也可以把它理解成“对每个权重 $w$ 直接惩罚它的平方”，在目标函数里额外加上：

$\frac{1}{2}\lambda w^2$

之所以经常写成 $\frac{1}{2}$ 的形式，是因为这样对 $w$ 的梯度更干净：

$\frac{\partial}{\partial w}\left(\frac{1}{2}\lambda w^2\right)=\lambda w$

从梯度下降更新角度看，L2 正则会让权重在每次更新时都被“线性拉回到 0”（weight decay）：

$W \leftarrow W - \eta\left(\nabla_W L_{data} + \lambda W\right)$

其中 $\eta$ 是学习率。直觉上，L2 会更强烈地惩罚“尖峰/很极端”的权重向量，偏好更小、更分散（diffuse）的权重，从而鼓励网络“每个输入维度都用一点”，而不是“少数维度用得很猛”。
加入正则项后，Multiclass SVM 的总损失通常写成：

$L = \underbrace{\frac{1}{N}\sum_i L_i}_{\text{data loss}} + \underbrace{\lambda R(W)}_{\text{regularization loss}}$

把 $L_i$ 展开：

$L = \frac{1}{N}\sum_i \sum_{j\ne y_i} \max\big(0,\; f(x_i;W)_j - f(x_i;W)_{y_i} + \Delta\big) \; + \; \lambda\sum_k\sum_l W_{k,l}^2$

其中 $N$ 是样本数， $\Delta$ 是 margin（通常设为 1）， $\lambda$ 是正则强度（一般靠交叉验证/验证集挑）。

P2： $\lambda$ 对模型拟合效果的影响

把正则项加进去，除了“消除尺度歧义”以外，还有一个更重要的收益：
惩罚大权重往往能提升泛化。因为当权重很大时，某个输入维度的微小变化就可能强烈影响分数，模型更容易记住训练集里的噪声。

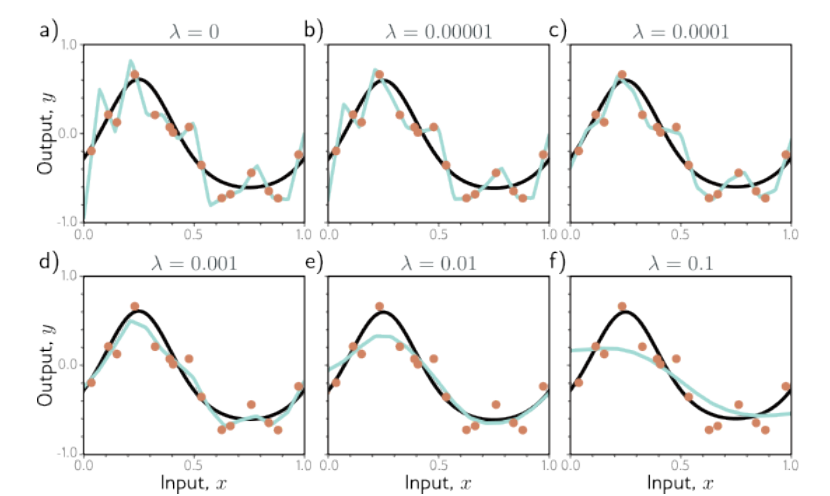
在上图中，黑色曲线代表真实的函数，橙色数据点代表加噪声的训练数据，青色曲线则是拟合出的模型。 $\lambda$ 较小时拟合函数倾向于精确的穿过所有数据点，但更容易记住噪声（过拟合）； $\lambda$ 过大时则产生的曲线过于平滑（欠拟合）。示例中 $\lambda = 0.001$ 下表现出了比较接近原函数的拟合效果。这种思想在课中多次提到：降低模型在训练数据上的表现来让它在测试数据中表现得更好。

一个经典直觉例子：设 $x=[1,1,1,1]$ ，两组权重 $w_1=[1,0,0,0]$ ， $w_2=[0.25,0.25,0.25,0.25]$ ，二者点积相同， $w_1^Tx=w_2^Tx=1$ ；但 L2 惩罚不同， $\lVert w_1\rVert_2^2=1$ ，而 $\lVert w_2\rVert_2^2=0.25$ 。因此在同样拟合数据的前提下，L2 会偏好 $w_2$ 这种“更小、更分散”的权重。

bias 要不要正则化 常见做法是只正则化权重 $W$ ，不正则化 bias $b$ 。理由是： $W$ 控制每个输入维度对分数的影响强度，而 $b$ 主要做整体平移。不过实际里把 $b$ 一起正则化通常影响不大。
为什么加了正则之后总 loss 很难到 0 即使数据项能到 0，总损失还会剩下 $\lambda R(W)\ge 0$ 。只有 $W=0$ 才可能让 $R(W)=0$ ，但这显然无法分类，所以一般不会期待总损失精确为 0。

P3：L1正则化与L2正则化

最常见的两种正则化是 L2（Ridge/weight decay）和 L1（Lasso）：

$\mathrm{Penalty}_{L2}=\lambda\sum_{i=1}^{n} w_i^2$

$\mathrm{Penalty}_{L1}=\lambda\sum_{i=1}^{n} |w_i|$

两种回归的特性：

L2（岭回归）：倾向让所有权重都“整体变小、更平滑”，但通常不会把权重压成精确的0；优化稳定、最常用。
L1（Lasso）：更容易产生稀疏解（很多权重被压到精确 0），相当于自动做了特征选择，适合特征维度很高、希望模型更“简洁”的场景。

课里也强调了一个实践经验：如果你并不关心显式的特征选择（feature selection），通常 L2 会比 L1 更稳、更常用，效果也往往更好；而 L1 更像是“顺带做特征筛选”的正则。

Elastic Net（L1 + L2）

L1 和 L2 可以组合使用（Elastic Net Regularization）：

$R(W)=\lambda_1\lVert W\rVert_1 + \lambda_2\lVert W\rVert_2^2$

它兼具两者的一些优点：L1 带来稀疏性倾向，L2 让优化更稳定、权重更平滑。在特征高度相关、又希望模型别太“极端稀疏”的时候，Elastic Net 是一个常见折中。

为什么 L1 更容易得到稀疏解，一个经典解释来自几何直觉（把原始损失等高线和正则约束边界放在一起看）：

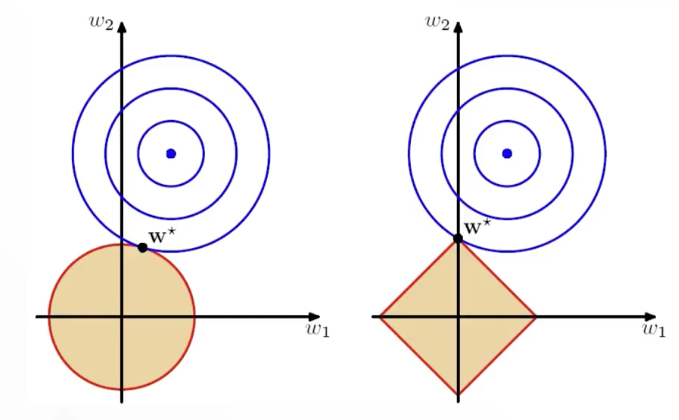
L2 的约束形状像圆： $\sum_i w_i^2\le C$ ，边界光滑，等高线与它相切的点很难刚好落在坐标轴上，所以权重通常不为 0。
L1 的约束形状像菱形： $\sum_i |w_i|\le C$ ，有尖角且尖角落在坐标轴上，等高线更容易先碰到尖角，从而得到某些维度恰好为 0。

从梯度/次梯度也能记住这个差异：

L2 对 $w_i$ 的梯度是 $2\lambda w_i$ ，当 $w_i\to 0$ 时梯度也趋近 0，推动它“继续变小”的力会变弱。
L1 对 $w_i$ 的次梯度是 $\lambda\,\mathrm{sgn}(w_i)$ （在 0 附近仍是常量级），会持续把权重往 0 推，更容易把不重要的维度压成 0。

特性	L1（Lasso）	L2（Ridge）
惩罚项	权重绝对值的和	权重平方和
权重结果	稀疏（很多变 0）	平滑（普遍变小但不为 0）
主要作用	特征选择 + 防过拟合	防过拟合（更稳）
优化难度	相对更麻烦（不可导点）	相对更容易

Max Norm Constraints（最大范数约束）

除了在目标函数里加惩罚项，还可以对每个神经元的权重向量施加硬约束：

$\lVert \vec{w} \rVert_2 \le c$

训练时用“投影梯度下降”（Projected Gradient Descent）的思路实现：先照常做一次参数更新，然后把每个神经元的权重向量按需缩放/截断到球内（clamp）。典型的 $c$ 取值在 3 或 4 的量级。

一种常见的实现写法是对每个神经元的权重向量做投影：

$\vec{w} \leftarrow \vec{w}\cdot\min\left(1,\;\frac{c}{\lVert \vec{w}\rVert_2}\right)$

这个做法的一个直观优点是：即使学习率设得偏大，权重也不容易“爆炸”（explode），因为每一步都会被约束到有界范围内。

P4：代码

这里的“向量化”指的是：把原本用 Python for 循环逐元素/逐类别/逐样本计算的部分，改写成 NumPy 的批量张量运算（矩阵乘法、广播、maximum、按索引取值等），让底层用优化过的 C/BLAS 去跑。

Unvectorized：主要计算靠显式循环完成（最慢但最直观）。在下面的 L_i 中，对“类别维度 $C$ ”使用 for j in range(C) 逐类累加。
Half-vectorized：把某一维（通常是类别维度 $C$ ）的循环去掉，仍保留另一维（通常是样本维度 $N$ ）的循环。这里 L_i_vectorized 对单样本不再遍历类别，而是一次性算出所有类别的 margin。
Fully-vectorized：把类别维度 $C$ 和样本维度 $N$ 的循环都去掉，直接对整批数据做矩阵运算；这是作业/工程里最常见的高性能写法。

import numpy as np

def L_i(x, y, W):
  """
  Unvectorized: multiclass SVM loss for one example (x, y)

  逐行理解这段代码的关键：
  1) 先算出每个类别的 score（线性分类器 f(x;W)=Wx）。
  2) 对所有“错误类别 j != y”，计算 margin = score[j] - score[y] + delta。
  3) hinge loss 取 max(0, margin)，再对所有错误类求和。

  参数/形状约定：
  - x: 单样本特征向量（常写成列向量 D x 1；也可能是一维 (D,)）
  - y: 正确类别下标（int，范围 [0, C)）
  - W: 权重矩阵 (C, D)，每一行对应一个类别的权重
  """
  delta = 1.0  # margin 超参数 Δ，SVM 里常固定为 1
  scores = W.dot(x)  # 计算所有类别的分数：scores 形状通常是 (C,) 或 (C, 1)
  correct_class_score = scores[y]  # 取出正确类别 y 的分数 score_y
  C = W.shape[0]  # 类别数 C（也就是 W 的行数）
  loss_i = 0.0  # 当前样本的损失初始化
  for j in range(C):  # 逐类别遍历（这是“非向量化”的瓶颈之一）
    if j == y:  # 正确类不参与 hinge loss 求和
      continue
    # hinge loss：只在 margin>0 时产生损失；否则这一类对 loss 贡献为 0
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i  # 返回单样本损失（还没除以 N，也还没加正则项）


def L_i_vectorized(x, y, W):
  """Half-vectorized: no loop over classes for one example.

  “半向量化”的意思：
  - 仍然是“单个样本”的损失（所以外层通常还会对样本循环 N 次）
  - 但把“对类别 j 的循环”去掉，用一次 NumPy 向量运算算出所有 margin
  """
  delta = 1.0  # Δ
  scores = W.dot(x)  # (C,) 或 (C,1)
  # scores - scores[y] + delta：对所有类别同时计算 margin_j = score_j - score_y + Δ
  # np.maximum(0, ·)：实现 hinge 的 max(0, margin)
  margins = np.maximum(0, scores - scores[y] + delta)
  margins[y] = 0  # 正确类的 margin 按定义不计入损失（把它强制置 0）
  loss_i = np.sum(margins)  # 对所有类别的 hinge loss 求和得到单样本损失
  return loss_i


def L(X, y, W):
  """
  Fully-vectorized (exercise style):

  Fully-vectorized 的核心：把“样本维 N”和“类别维 C”的循环都去掉。

  形状约定（这点非常关键，否则索引会看不懂）：
  - X 把所有训练样本按“列”堆起来：X 是 (D, N)
    - D: 特征维度
    - N: 样本数
  - y 是 (N,)：第 i 个样本的正确类别是 y[i]
  - W 是 (C, D)
  """
  delta = 1.0  # Δ
  scores = W.dot(X)  # (C, D)@(D, N) -> (C, N)，第 j 行第 i 列是第 i 个样本对类 j 的分数
  N = X.shape[1]  # 样本数 N（因为样本按列放）
  y = np.asarray(y).ravel()  # 确保 y 是一维形状 (N,)，便于后面的花式索引

  # 取出每个样本的正确类分数 score_{y_i}：
  # - np.arange(N) 生成 [0,1,...,N-1]
  # - scores[y, np.arange(N)] 等价于对每列 i 取行 y[i]
  correct_scores = scores[y, np.arange(N)]  # (N,)

  # 计算所有 (j, i) 的 margin：margin_{j,i} = score_{j,i} - score_{y_i,i} + Δ
  # 这里会发生广播（broadcast）：
  # - scores 是 (C, N)
  # - correct_scores 是 (N,)
  # NumPy 会把 (N,) 视作 (1, N)，从而在类别维 C 上自动复制，得到 (C, N)
  margins = np.maximum(0, scores - correct_scores + delta)  # (C, N)

  # 正确类不参与损失：对每个样本 i，把 j=y[i] 的那一项置 0
  margins[y, np.arange(N)] = 0

  loss = np.sum(margins) / N  # 对所有样本、所有错误类求和，再除以 N 得到平均 data loss
  return loss

把 L2 正则加进去，核心就是：

$L = L_{data} + \lambda\sum_{k,l}W_{k,l}^2$

对应代码就是在数据损失后加上 reg * np.sum(W * W)（很多实现把 $\lambda$ 命名为 reg）：

def svm_loss_with_l2(X, y, W, reg=1e-3):
  """带 L2 正则的 multiclass SVM 损失（向量化版本）。

  这段代码分两部分：
  - data_loss：hinge loss（来自数据）
  - reg_loss：L2 正则项（来自参数），也常被叫 weight decay

  这里把正则强度 λ 命名为 reg（与不少作业/代码库一致）。
  """
  delta = 1.0  # Δ
  scores = W.dot(X)  # (C, D)@(D, N) -> (C, N)
  N = X.shape[1]  # 样本数

  # 取正确类分数 (N,)
  correct_scores = scores[y, np.arange(N)]

  # 广播得到所有 margin，再做 hinge
  margins = np.maximum(0, scores - correct_scores + delta)  # (C, N)
  margins[y, np.arange(N)] = 0  # 正确类置 0

  data_loss = np.sum(margins) / N  # 平均数据损失

  # L2 正则：sum_{k,l} W_{k,l}^2
  # 写成 W*W 是逐元素平方；np.sum 汇总所有元素
  reg_loss = reg * np.sum(W * W)

  return data_loss + reg_loss  # 总损失 = 数据损失 + 正则损失