CS231n笔记04:优化与梯度下降
统一记号:
- 目标函数(loss):,参数向量:
- 第 次迭代(iteration)参数:
- 梯度:
- 学习率:(或 )
- mini-batch:,其梯度估计记为
P1:优化器
优化器是在反向传播给出梯度之后,决定“参数往哪里走、走多远”的更新规则,一个最常见的形式是损失最小化:
反向传播(backprop)负责高效地算出梯度 ;优化器负责把梯度变成一次次参数更新。
P2:Vanilla GD(批量梯度下降,Batch Gradient Descent)
最朴素的梯度下降每次用全量数据计算精确梯度,然后沿负梯度更新:
优点:
- 梯度精确、更新方向稳定;对凸问题有清晰理论。
缺点:
- 每步都要扫全数据集,代价高;大模型/大数据下几乎不可用。
- 对非凸深网也不具备“逃离坏点”的随机性。
P3:SGD(随机梯度下降,Stochastic Gradient Descent)
SGD 每次只用一个样本(或极小 batch)来计算梯度:
优点:
- 单步开销小、更新频繁;在大数据下非常高效。
- 梯度噪声有时反而有益:更容易“抖”出鞍点或糟糕的局部区域。
缺点(直觉上也最常见):
- 更新噪声大,loss 曲线抖动明显。
- 在狭长沟壑(某些维度很陡、某些维度很平)中容易来回震荡。
- 在鞍点附近(一个方向上凸、另一个方向上凹)可能进展很慢。
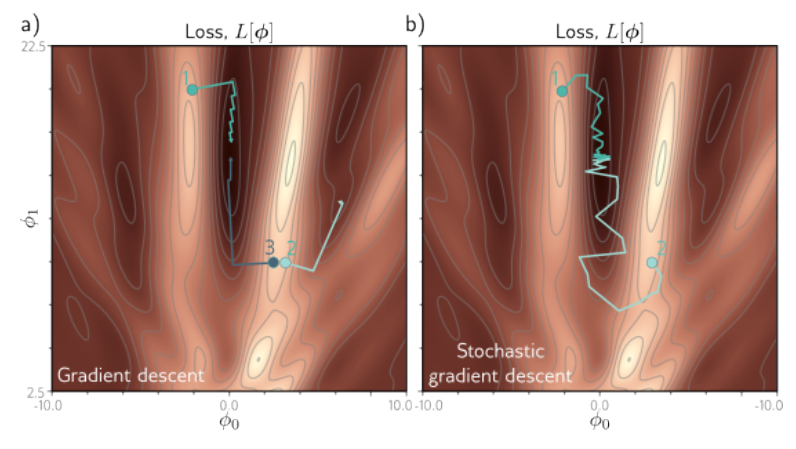
图 a) 中,起点的位置会影响梯度下降的结果:在点1,3处,参数梯度下降到了全局最小值,而在2处,错误的起点使其下降到了局部最小值。在图b)中,SGD的更新方向由于噪声的存在而变得不稳定,从而使得参数能够跳出鞍点区域,继续向下优化。
P4:Mini-batch SGD
实践中最常见的是 mini-batch SGD:用一个小批量 估计梯度:
它介于 GD 和 SGD 之间:
- batch 变大 → 梯度方差更小、更新更稳,但单步更贵。
- batch 变小 → 更新更“吵”,探索更强,但可能更难调、吞吐不一定更高。
工程里通常按硬件吞吐与收敛稳定性折中选 batch size;并配合学习率缩放(例如线性缩放)与 warmup。
P5:SGD with Momentum(动量法)
动量法的核心是引入“速度”变量 (一阶动量),对梯度做指数滑动平均,从而减少震荡并加速沿一致方向的前进:
其中 是动量系数,常见经验值是 0.9。
优点:
- 在“长沟壑”场景明显加速;抑制来回震荡。
- 比 vanilla SGD 更稳、更好调。
缺点:
- 仍可能在某些非凸区域走得过头(overshoot)。
- 额外超参数()与更复杂的调度策略。
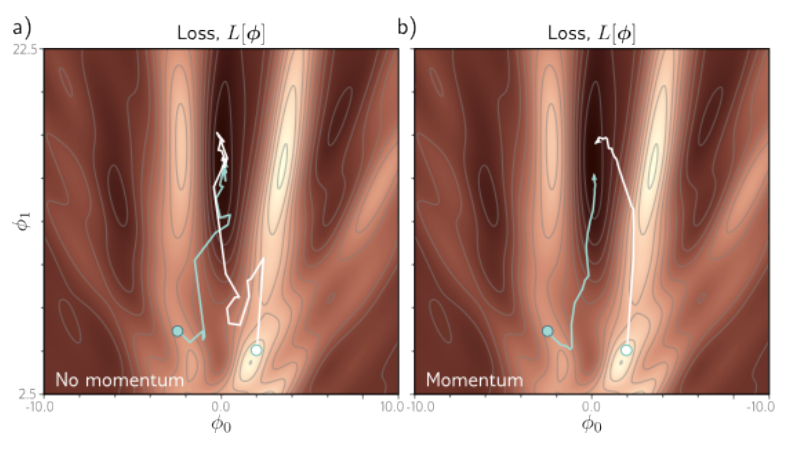
直观上看无动量的随机梯度下降以非直接的路径接近最小值,而有动量的随机梯度下降则由前一段优化方向和当前batch的梯度加权组合产生,可以平滑轨迹加快收敛。
P6:Nesterov Momentum(NAG,Nesterov 加速梯度)
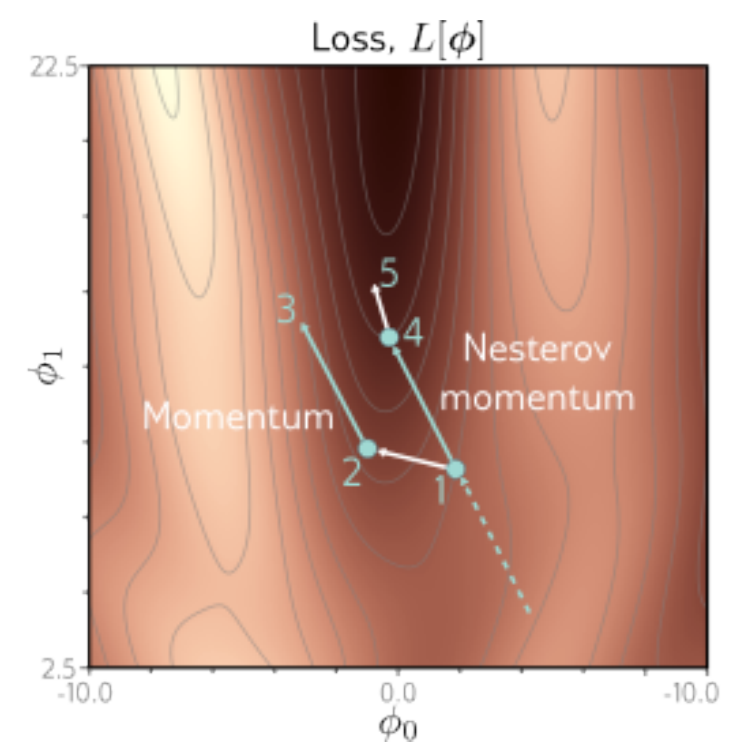
Nesterov 的直觉是“先按动量往前看一步,再在那个位置上评估梯度”,因此更像是在用更前瞻的梯度修正动量方向。
一种常见写法是:
优点:
- 在很多任务上比普通 Momentum 稍稳,收敛更“聪明”。
缺点:
- 仍需调学习率与动量。
Second-order methods(二阶方法)
深度学习优化里还有一类很常见的思路是基于 Newton’s method(二阶方法),其核心迭代为:
其中 是 Hessian 矩阵(由二阶偏导数组成的方阵), 是梯度向量。直觉上,Hessian 描述了损失函数的局部曲率:乘上 Hessian 的逆,会让优化在“曲率较小(更平坦)”的方向迈更大步,在“曲率较大(更陡)”的方向迈更小步。注意这个更新式里没有显式学习率超参数,这也是二阶方法常被拿来对比一阶方法的一个优点。
但在深度学习里直接计算并求逆 Hessian 往往不可行:时间和空间开销都极其昂贵。比如一个有 100 万参数的网络,Hessian 是 的矩阵,显式存储就需要约 3725 GB 内存。
因此出现了大量 quasi-Newton(拟牛顿)方法来近似 。其中最常见的是 L-BFGS:它利用一段时间内的梯度信息来隐式构造近似(不显式存整张矩阵)。
但即使缓解了内存问题,L-BFGS 的一个朴素应用仍然通常需要在全量训练集上工作;而把它可靠地用在 mini-batch 上更困难,至今仍是研究/工程上的活跃方向。
所以在大规模深度学习与 CNN 训练中,目前更常见的仍是基于(Nesterov)Momentum 的 SGD 变体:实现更简单、扩展性更好。
P7:AdaGrad(自适应学习率:累积平方梯度)
AdaGrad 的动机是:不同参数维度的更新频率差异很大(例如稀疏特征/embedding),希望“常更新的参数走慢点,少更新的参数走快点”。
做法:对每个参数维护平方梯度累积 :
其中 、、除法都是逐元素(element-wise), 防止除 0。
优点:
- 在稀疏特征场景非常强;对每个参数都有自适应步长。
缺点:
- 单调增大,导致有效学习率单调衰减,训练后期可能“走不动”。
P8:RMSProp(自适应学习率:滑动平均平方梯度)
RMSProp 可以看作对 AdaGrad 的“降温”:不再把所有历史平方梯度都累积进去,而是用指数滑动平均跟踪一个有限时间尺度内的平方梯度。远离当前时间点的梯度信息会被逐渐丢弃,从而避免学习率过快衰减的问题。
其中 常取 0.9 或 0.99。
优点:
- 避免 AdaGrad 学习率过快衰减;在很多深网任务上表现稳定。
缺点:
- 仍需要调学习率;不同任务对 也可能敏感。
P9:AdaDelta(自适应学习率:进一步减少对初始学习率依赖)
AdaDelta 也是“滑动窗口”的思想:它在 RMSProp 的基础上,进一步把更新步长做得更自洽,尽量减少对手工设定初始学习率的依赖。
一种常见的表达是同时跟踪:平方梯度的滑动平均 与平方更新量的滑动平均 :
优点:
- 经验上更不容易出现“有效学习率衰减到 0”的尴尬。
缺点:
- 现代深度学习中常被 Adam/AdamW 取代;生态与默认配置更少。
P10:Adam(Adaptive Moment Estimation)
Adam 可以理解为:
- Momentum:对梯度做一阶动量(均值)的滑动平均
- RMSProp:对平方梯度做二阶动量(方差规模)的滑动平均
更新(逐元素)为:
由于 会导致早期偏置(bias),使得初始动量过大,Adam 通常使用偏置修正:
初始时将 和 放大,抵消 和 靠近 0 的影响。随着时间推移,修正项趋近于1,对原始动量的影响减小。
最终更新:
经验默认值常见为:。
优点:
- 收敛快、对学习率不那么敏感;新任务上很适合快速跑通 baseline。
潜在缺点(常见讨论点):
- 在部分设置下可能出现训练后期震荡或泛化不如精调的 SGD 系列。
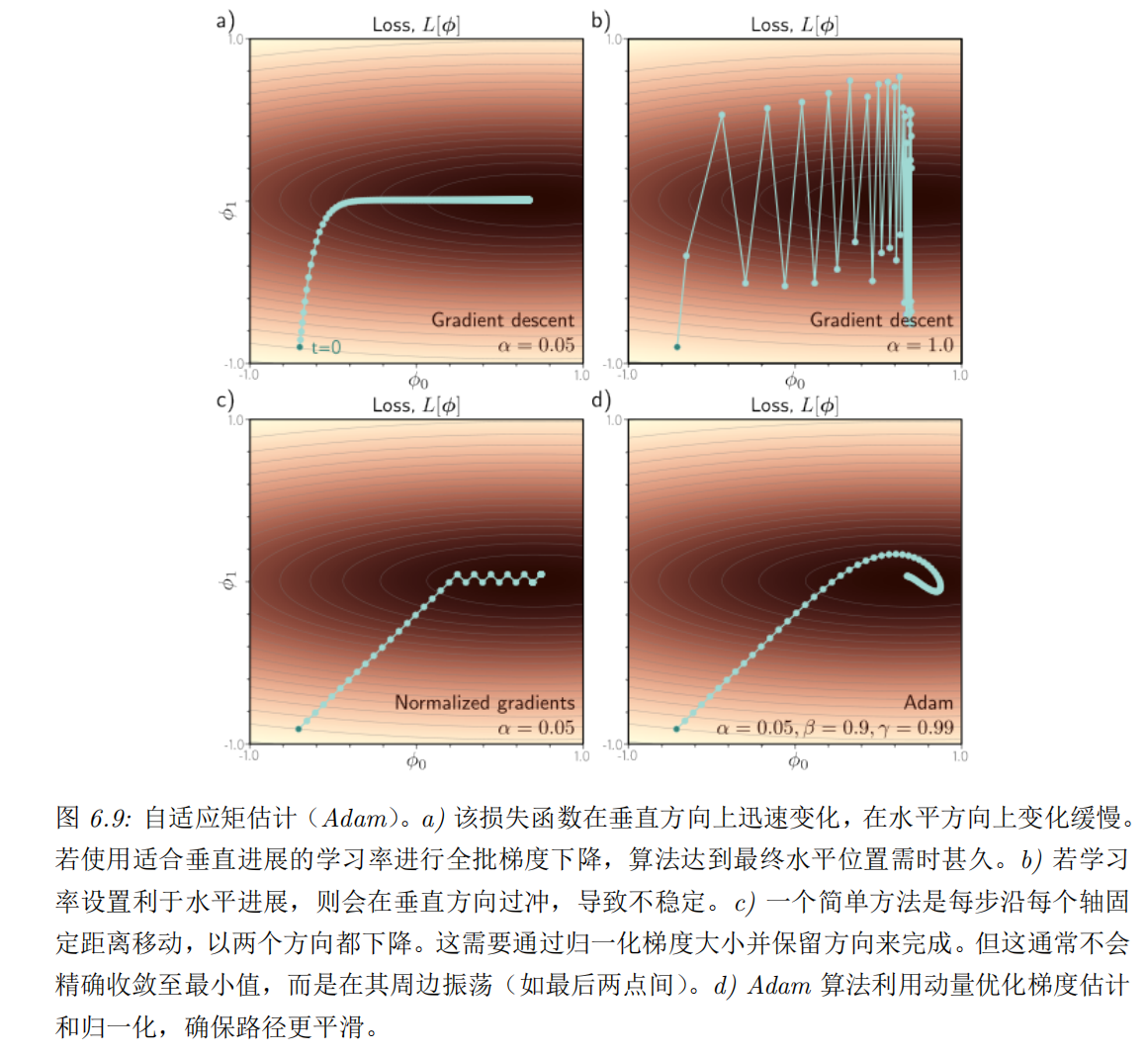
还有note上的动图:
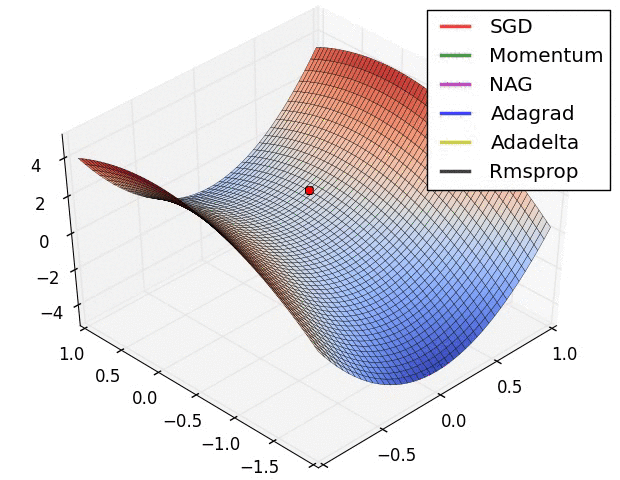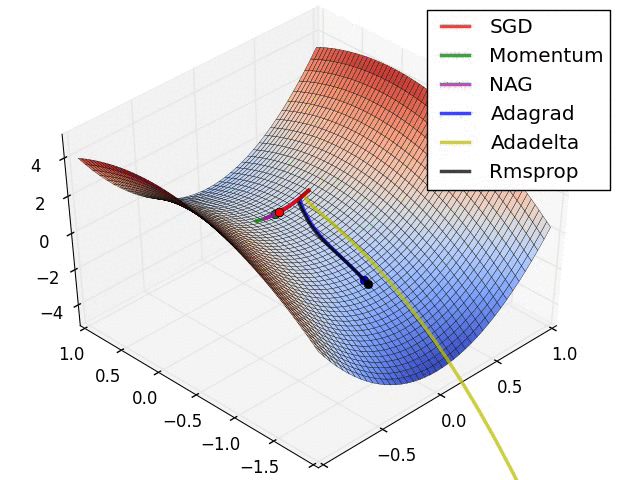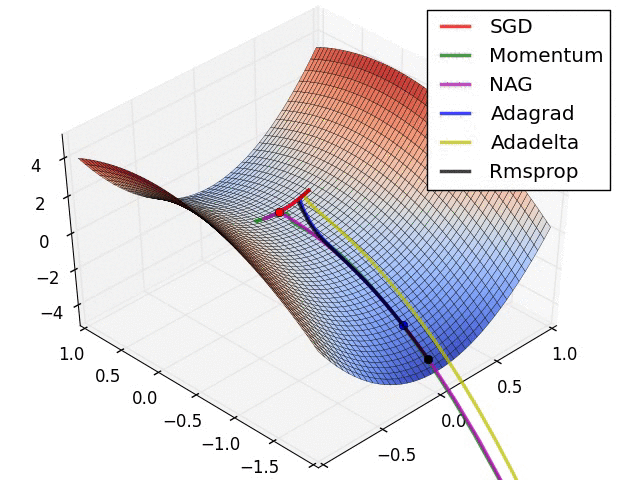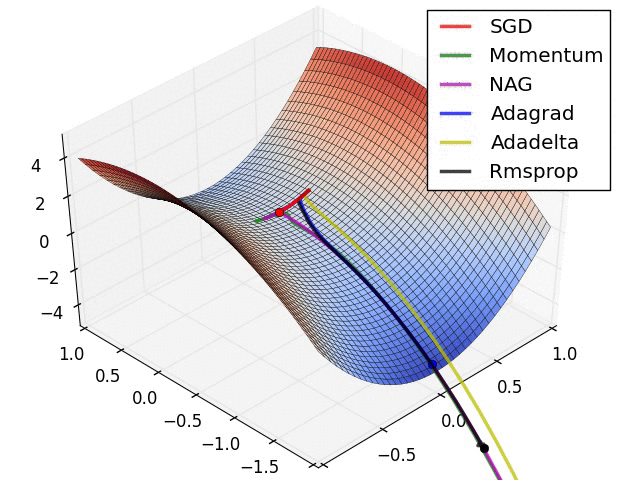
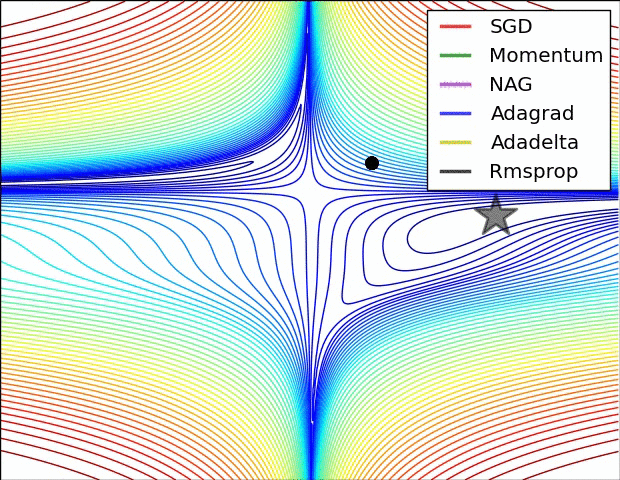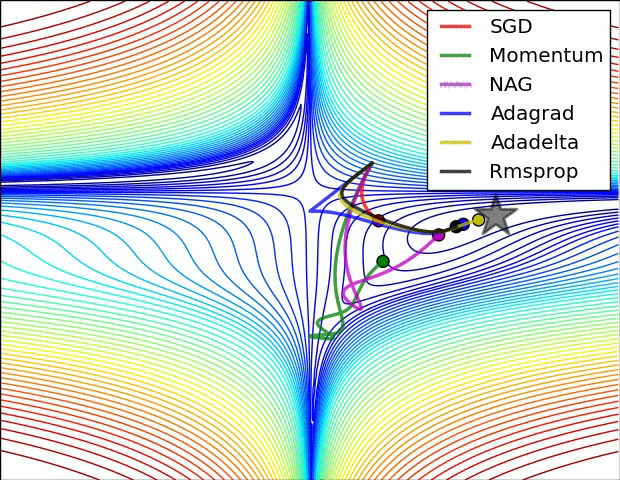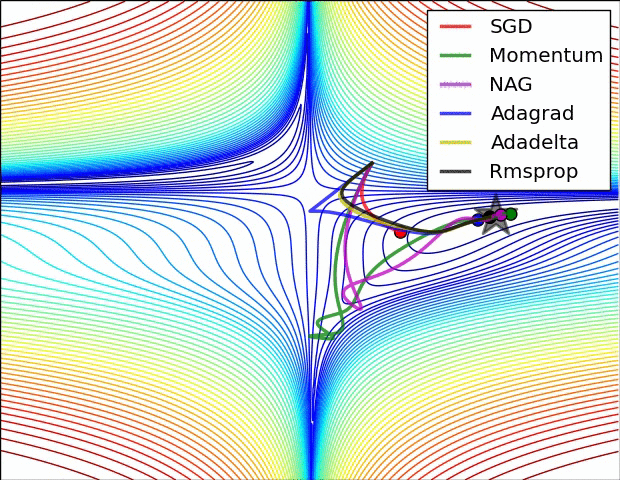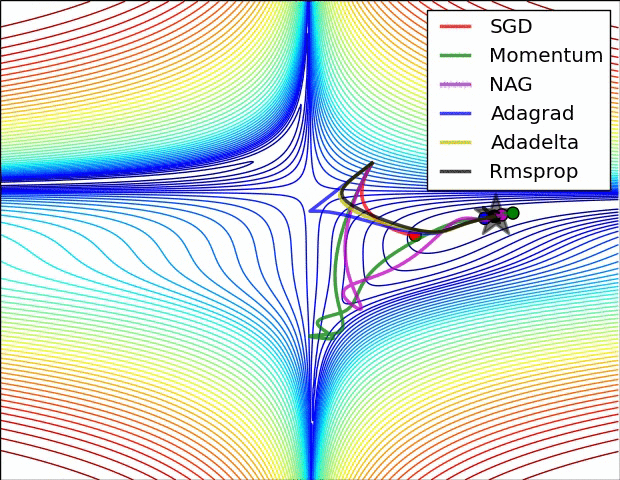
P11:Nadam(Nesterov + Adam)
Nadam 把 Nesterov 的“lookahead”思想融入 Adam 的一阶动量中,本质上是用更前瞻的方式来计算动量项,从而在一些任务上获得更快或更稳的收敛。
一个常用、也比较容易和代码对齐的 Nadam(带 bias correction)可以写成:
先算 Adam 的动量与偏置修正:
然后把 Nesterov 的“lookahead”体现在一阶动量上(把它看作一个更前瞻的一阶动量项):
最终参数更新:
实现上常见做法是对 的使用方式做 Nesterov 风格的修正(不同实现细节略有差异),但核心思想可以记作一句话:Adam 负责“自适应步长 + 动量”,Nadam 负责“在动量上再更前瞻一点”。
优点:
- 有时比 Adam 更快、更稳。
缺点:
- 并非总是优于 Adam;生态不如 AdamW 常用。
P12:AdamW(Decoupled Weight Decay)
在很多代码里你会看到把 L2 正则写进 loss:
这会让梯度多出一项 。
但对 Adam 这类自适应方法来说,“把 L2 正则并入梯度”与“做权重衰减(weight decay)”并不完全等价。
AdamW 的核心就是把权重衰减从梯度里解耦出来,直接在参数更新时做衰减:
优点:
- 在大量任务里比 Adam + L2 更稳,泛化更好;现代训练中非常常用。
P13:学习率调度(Learning Rate Scheduler)
很多时候,“用什么优化器”不如“学习率怎么随时间变化”重要。一个常用经验是:
- 前期需要更大的学习率来探索与快速下降
- 后期需要更小的学习率来稳定收敛到更好点
下面列几类常见调度方式(它们可与上面任何优化器组合):
1)Step decay(阶梯衰减)
每隔若干 epoch 把学习率乘一个系数 :
优点是简单、超参数好解释;缺点是学习率跳变可能带来波动。
2)Exponential decay(指数衰减)
更平滑,但需要合适的 。
3) decay
衰减更温和,经典但不一定是最佳。
4)Cosine decay(余弦退火)
在现代训练(尤其是视觉任务)中非常常见:
5)Warmup
无论用哪种 decay,大 batch 或大模型训练常常会在前几百/几千 step 用 warmup:
- 从很小的学习率线性/非线性升到目标学习率
- 减少初期不稳定与梯度爆炸风险







