CS231n笔记06:卷积层
在之前的神经网络中,使用了全连接层来处理输入数据。然而,对于图像等具有空间结构的数据,这种网络将图像拉伸成了一个一维向量,向量中的每一个元素的地位是相同的,抛弃了原始图像中像素的位置信息。卷积神经网络(Convolutional Neural Networks, CNNs)通过引入卷积层,能够更好地利用图像的空间结构信息,从而提升模型的性能。
P1:卷积
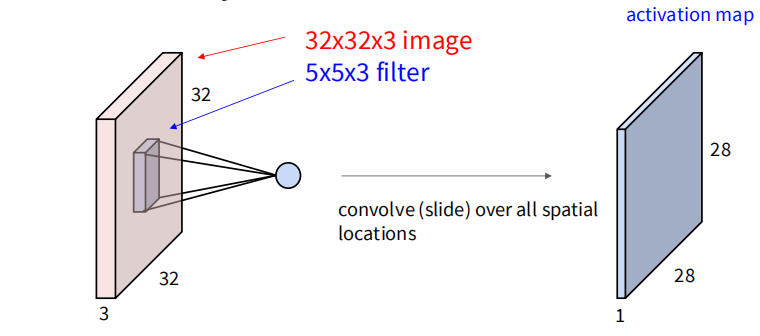
首先考虑一张图片,宽度为 ,高度为 ,通道数为 (此处 RGB 图像的 )。卷积操作使用一个大小为 的卷积核(filter 或 kernel)的权重矩阵在图像上滑动,对图像的局部区域进行加权求和,从而提取特征。假设卷积核每次在图像上移动1个像素,那么卷积核每一次运算产生一个标量,通过在原图上滑动卷积核,可以得到一个新的Activation Map,大小为 ,厚度为1。
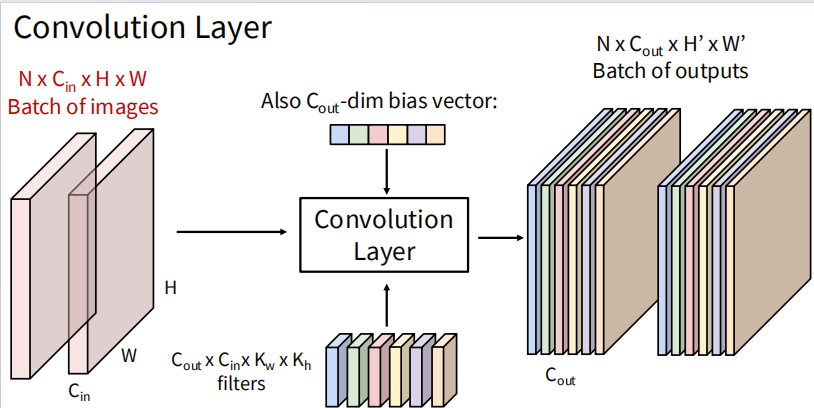
进一步拓展,使用多个卷积核来提取不同的特征。假设使用 个卷积核,那么每个卷积核都会生成一个 Activation Map,最终将这些 Activation Map 堆叠起来,形成一个大小为 的输出。这样,卷积层就能够从输入图像中提取出多种不同的特征。再将输入变为多张图片组成的 batch,输入尺寸为 ,输出尺寸为 。

实际构建卷积层时,还需要添加激活函数。浅层的卷积层学习图像的一些边缘,纹理,颜色特征;而深层的卷积层则倾向于学习更复杂的形状和对象部分。通过多层卷积层的堆叠,卷积神经网络能够逐渐提取出图像中越来越抽象和复杂的特征。

P2:填充与步幅
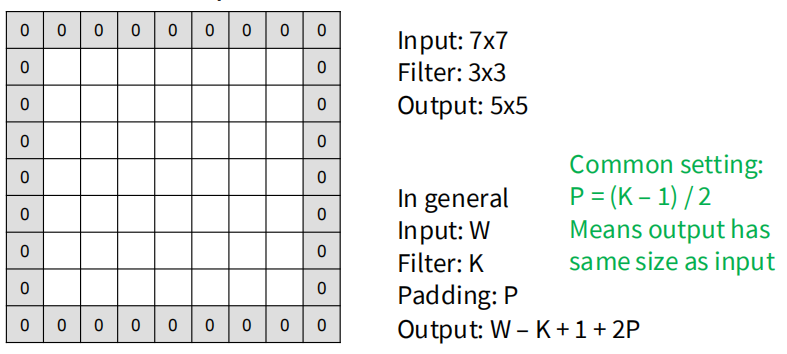
在实际应用中,为了控制卷积操作后输出的空间尺寸,通常会使用填充(padding)。填充是在输入图像的边缘添加额外的像素,通常是0值,以防止卷积操作导致输出尺寸过小。对于一个大小为 的卷积核,如果在输入图像的每一边都添加 行/列的填充,那么输出图像的尺寸将变为 。一般将填充层数设置成 ,可以保证输出尺寸与输入尺寸相同。
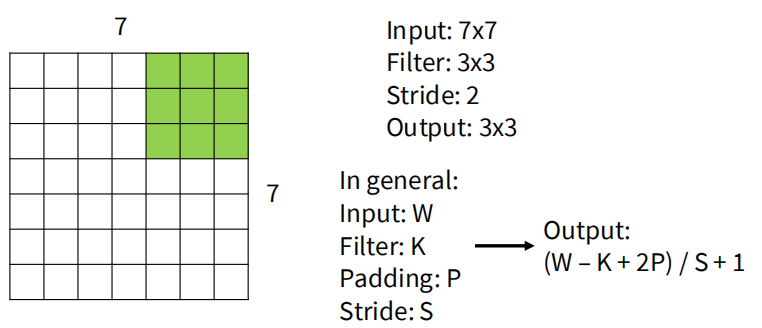
步幅是卷积核每次在图像上滑动的距离。默认情况下,步幅为1,即卷积核每次移动1个像素。如果将步幅设置为 ,那么输出图像的尺寸将变为 。增大步幅可以减少输出的空间尺寸,从而降低计算量,但可能会丢失一些细节信息。
P3:感受野
感受野(Receptive field)是指卷积神经网络中某一层的神经元能够“看到”的输入图像的区域大小。随着网络层数的增加,感受野会逐渐扩大,使得深层神经元能够捕捉到更大范围的图像信息。感受野的大小取决于卷积核的大小、填充和步幅等参数。较大的感受野有助于模型理解图像中的全局结构和上下文信息,从而提升分类和识别的性能。
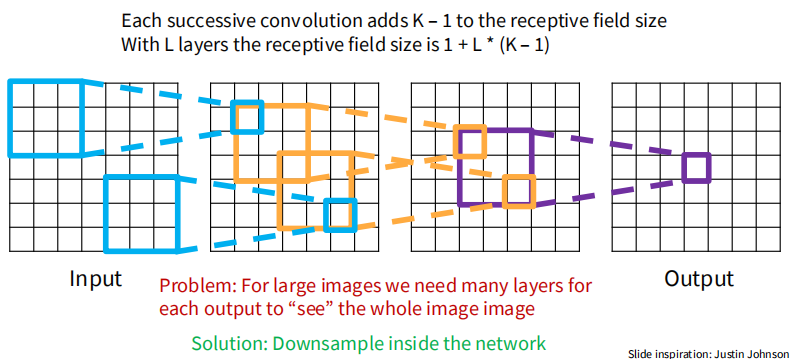
考虑步幅为1的情况,每经过一层卷积,感受野会增加 (卷积核大小减1)。如果有多层卷积堆叠在一起,感受野的计算可以通过累加每一层的贡献来完成。 层数下,考虑一般情况,感受野大小为:
P4:池化层
池化层(Pooling Layer)通常用于卷积神经网络中,用于降低特征图的空间尺寸,从而减少计算量和参数数量。常见的池化方法有最大池化和平均池化。
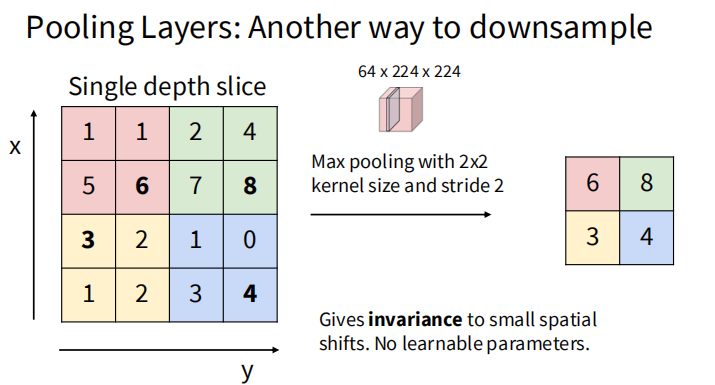
作为一种下采样方法,池化和卷积核不同,池化操作没有可学习的参数。最大池化通过选择池化窗口内的最大值来保留最显著的特征,而平均池化则计算窗口内的平均值。池化层通常紧跟在卷积层之后,帮助模型提取更具鲁棒性的特征。
P5:等变性
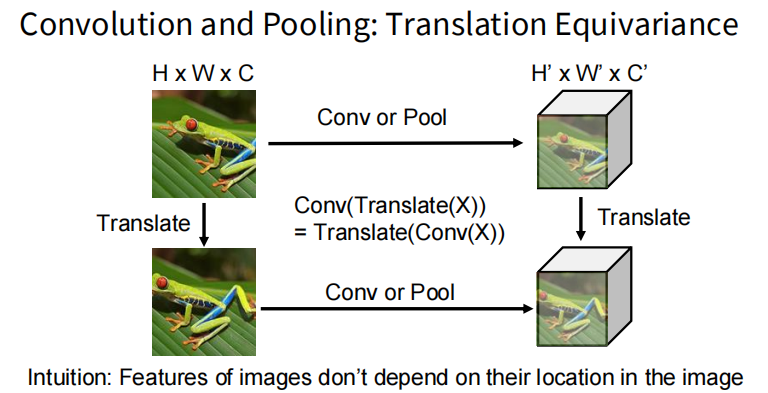
卷积操作具有平移等变性(translation equivariance),即当输入图像发生平移时,卷积层的输出也会相应地发生平移。这一特性使得卷积神经网络能够更好地处理图像中的位移变化,提高模型的泛化能力。然而,卷积操作对旋转和缩放等变换并不具备等变性。








