P1：卷积网络

标准化

在神经网络中，随着网络的加深，输入的分布会随着前一层参数的变化而变化，导致训练效率下降。这种现象导致模型必须使用更小的学习率和更谨慎的参数初始化。虽然非线性激活函数和小学习率等方法能部分缓解问题，但是无法从根本上解决分布变化带来的梯度消失或爆炸问题。因此引入标准化：

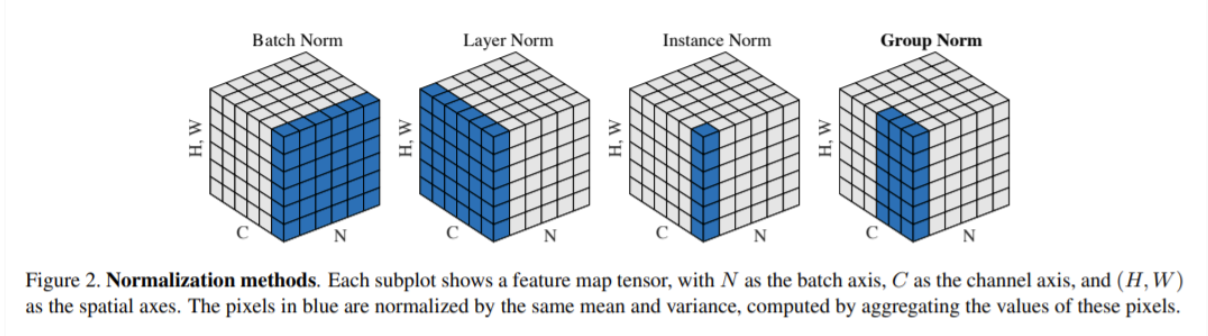
上图中总结了常用的标准化方法，其中H,W是特征图的高与宽，C为特征图通道数，N为Batch Size。标准化就是将数据变换为均值为0，方差为1的分布，然后再通过可学习的缩放和平移参数保留数据的表达能力，公式如下：

Normalization(x)=γx−μσ+β\text{Normalization}(x) = \gamma \frac{x - \mu}{\sigma} + \beta

其中μ,σ\mu, \sigma分别为均值和标准差，γ,β\gamma, \beta为可学习的缩放和平移参数。不同的标准化方法通过计算不同维度的数据均值和方差来实现对数据的标准化处理。

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
BN在每一个mini-batch上计算均值和方差，对每个特征维度进行标准化处理。BN的优点包括加速收敛、允许使用更高的学习率、减少对参数初始化的依赖等。BN通常在卷积层或全连接层之后，激活函数之前使用。其在某些情况下可以替代Dropout作为正则化手段。BN适用于卷积层和全连接层，尤其对深层网络效果显著。
Layer Normalization
LN对每一个样本的所有特征维度进行标准化处理。LN的优点包括不依赖于mini-batch大小，适用于RNN等序列模型，计算简单且易于实现，通常在RNN和Transformer等模型中使用。
Instance Normalization: The Missing Ingredient for Fast Stylization
IN在单个样本的单个特征通道上进行标准化处理，与batch与layer都无关。
Group Normalization
GN将特征通道划分为多个组，在每个组内进行标准化处理，与batch与layer无关。GN的优点包括适用于小批量训练，计算效率高，其在计算上介于IN和LN之间。

使用标准化方法的直觉是，无论从第一层出发的时候如何，也不管在训练过程中怎样偏离，都在每一层设置一个检查点减均值除方差，再进行缩放平移，强制每一层的输入分布保持稳定，从而稳定训练过程。使用这种方法时，大大降低了对于初始化的要求。即使没有使用He初始化这类方法，仍然能够提高网络训练的深度和速度。

Dropout

Dropout是一种常用的正则化手段，用于防止神经网络过拟合。其核心思想是在训练过程中随机“丢弃”一部分神经元，使得网络在每次前向传播时都使用不同的子网络进行训练，从而增强模型的泛化能力。

三层神经网络运用Dropout示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
p = 0.5

def train_step(X):
    H1 = np.maximum(0, mp.dot(W1, X) + b1)
    U1 = np.random.rand(*H1.shape) < p  # Dropout掩码
    H1 *= U1  # 应用Dropout
    H2 = np.maximum(0, mp.dot(W2, H1) + b2)
    U2 = np.random.rand(*H2.shape) < p  # Dropout掩码
    H2 *= U2  # 应用Dropout
    out = mp.dot(W3, H2) + b3
    # 省略向前传播和参数更新

def predict(X):
    # 缩放激活值，预测时不使用Dropout
    H1 = np.maximum(0, mp.dot(W1, X) + b1) * p
    H2 = np.maximum(0, mp.dot(W2, H1) + b2) * p
    out = mp.dot(W3, H2) + b3

激活函数

  • ReLU（Rectified Linear Unit）: f(x)=max⁡(0,x)f(x) = \max(0, x)，计算简单且收敛速度快，是目前最常用的激活函数。缺点是在负区间梯度为0，且输出不是零均值。
  • Sigmoid: f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}，输出范围在(0, 1)之间。缺点是过大的正值和过小的负值容易导致梯度消失，且输出不是零均值。Sigmoid的叠加会导致梯度消失问题。
  • GELU（Gaussian Error Linear Unit）: f(x)=xΦ(x)f(x) = x \Phi(x)，相比RELU在0附近更加平滑，能够缓解梯度消失问题。但对于过小负值仍然会导致梯度消失。同时计算复杂度远大于ReLU。

VGGNet

VGGNet使用多个连续的3x3卷积核堆叠来增加网络深度，从而提升模型的表达能力。VGGNet通过增加网络深度，能够更好地捕捉图像中的复杂特征，提高分类性能。

P2：残差网络

残差连接与残差块

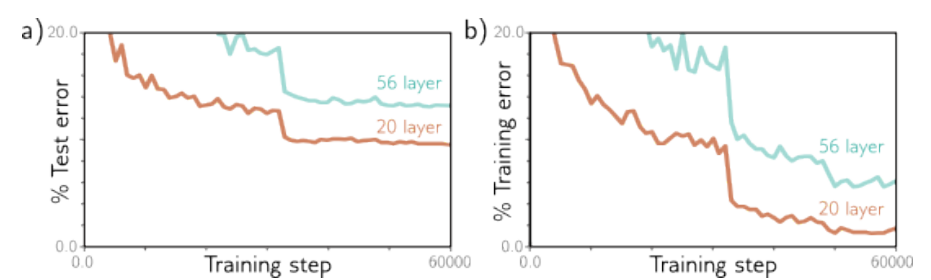
VGGNet有19层，性能超过了仅有8层的AlexNet，但随着网络深度的增加，图像分类性能在训练集和测试集上都下降了。这意味着问题在于训练更深的网络，而不是泛化能力不足。

下面一段摘自《Understanding Deep Learning》的原文：

对于这一现象，我们还没有完全理解其原因。一种推测是，初始化时，如果我们改变早期网络层中的参数，损失梯度会发生不可预测的变化。通过适当初始化权重，这些参数相对于损失的梯度应当是合理的，避免了梯度爆炸或消失的问题。然而，导数是基于参数的无限小变化，而优化算法实际上使用有限的步长。任何合理的步长选择都可能跳到一个完全不同、与原点梯度无关的位置上；损失表面更像是布满了无数微小山峰的广阔山脉，而不是一个易于下降的光滑结构。因此，优化算法无法像在梯度变化较慢时那样取得进展。
通过观察单输入单输出网络中的梯度，可以支持这种假设。对浅层网络而言，随着输入的变化，输出相对于输入的梯度变化得很慢（参见图 11.3a）。但对于深层网络，输入的微小改变就能导致一个截然不同的梯度（参见图 11.3b）。这一现象通过梯度的自相关函数得到了展示（参见图 11.3c）。在浅层网络中，相邻的梯度是相关的，但在深层网络中，这种相关性很快降至零，这就是所谓的梯度破碎现象。

残差网络通过在计算路径中添加分支，将各个网络层的输入加回到输出上，即f(x)=F(x)+xf(x) = \mathcal{F}(x) + x。这样做的好处是，即使某些层没有学到有用的特征，网络仍然可以通过恒等映射传递信息，从而缓解梯度消失问题。
在一个四层的残差网络中，将最终得到的输出展开，有：

y=x+f1[x]+f2[x+f1[x]]+f3[x+f1[x]+f2[x+f1[x]]]+f4[x+f1[x]+f2[x+f1[x]]+f3[x+f1[x]+f2[x+f1[x]]]]y = x + f_1[x] + f_2[x + f_1[x]] + f_3[x + f_1[x] + f_2[x + f_1[x]]] + f_4[x + f_1[x] + f_2[x + f_1[x]] + f_3[x + f_1[x] + f_2[x + f_1[x]]]]

放到图上看就是：

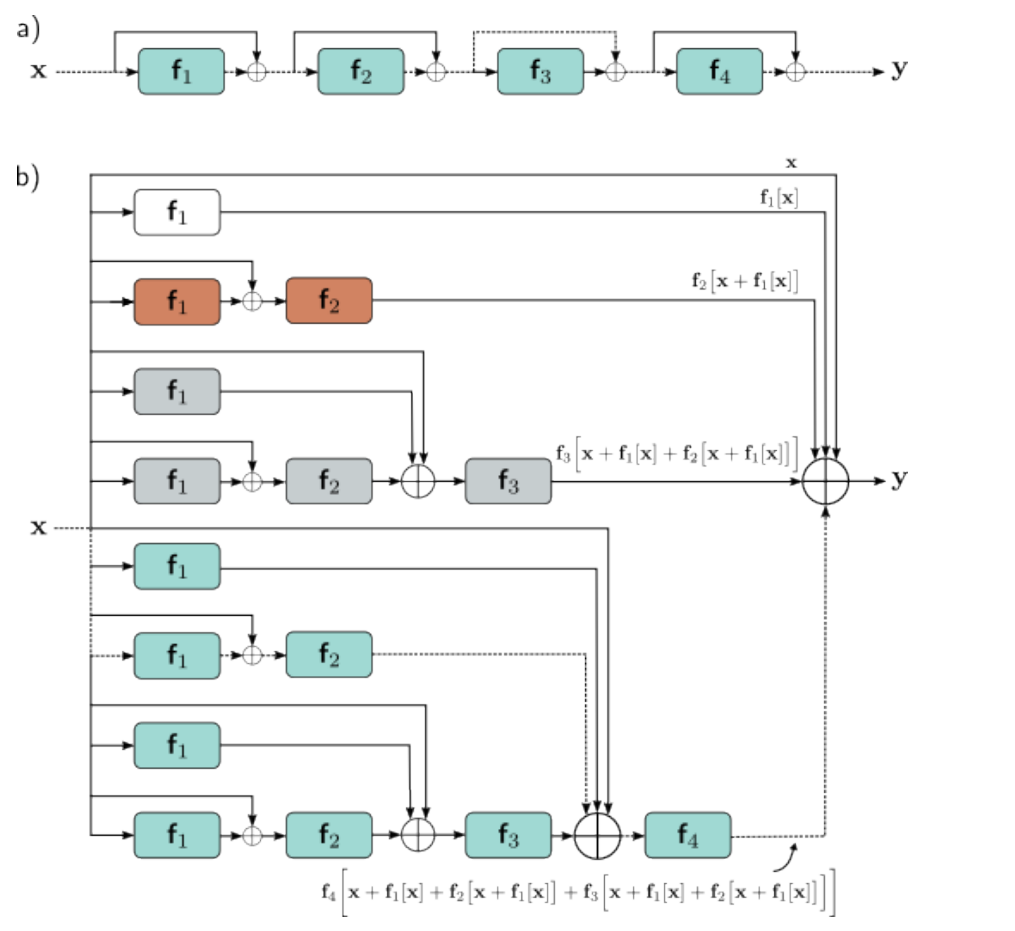
简单来说，就是每一层中参数的变化都直接贡献于网络输出y的变化，也通过不同长度的导数链间接做贡献。由于恒等项和各种短导数链将贡献于每层的导数，从而缓解了梯度消失问题。

ResNet

ResNet的核心思想如下：

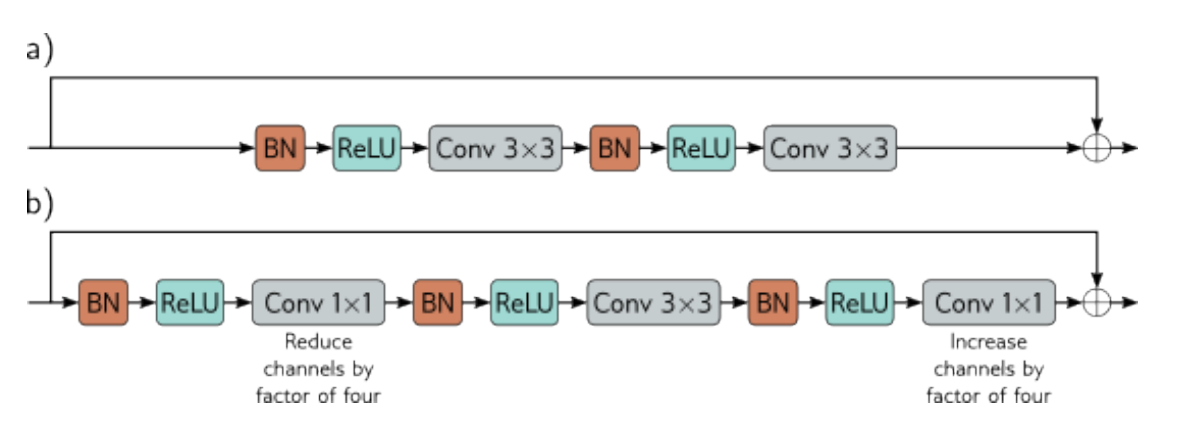
标准残差块包含批量归一化操作，然后是激活函数和3x3卷积层。瓶颈残差块则使用1x1卷积层来减少和恢复通道数，从而减少参数数量，降低计算复杂度。
ResNet-200 模型含有 200 层，用于在 ImageNet 数据库上进行图像分类。这个架构与 AlexNet 和 VGG 类似，但采用的是瓶颈残差块而非普通卷积层。与 AlexNet 和 VGG 相似，这些层周期性地交替减少空间分辨率并同时增加通道数。这里，分辨率通过步长为二的卷积进行下采样来降低。通道数的增加要么通过向表示添加零，要么通过额外的 1×1 卷积实现。网络的起始是一个 7×7 卷积层，随后是下采样操作。最终，一个全连接层将输出映射到一个长度为 1000 的向量上。这一向量通过 softmax 层生成类别概率。

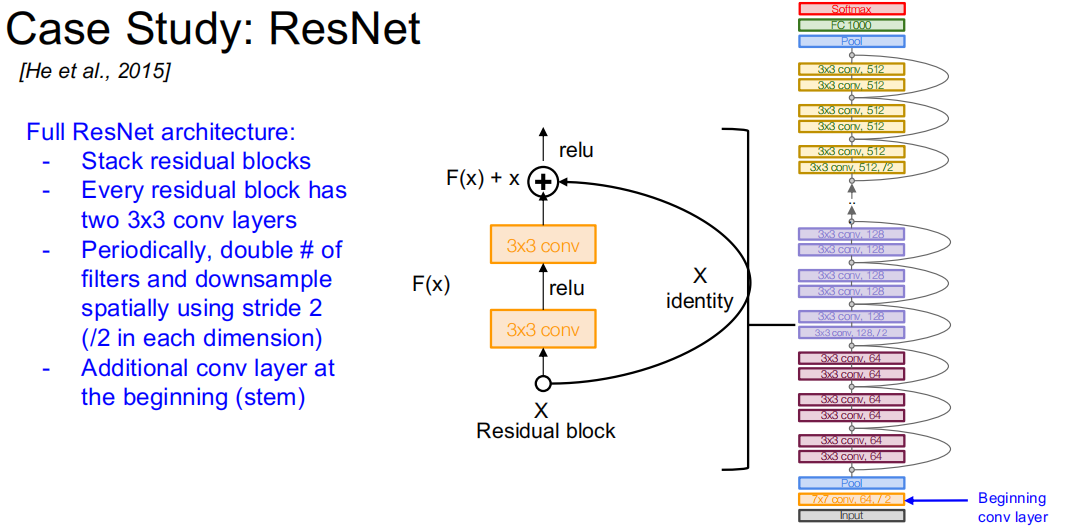
这个架构是2016年提出的，Top5错误率低至4.8%。目前最先进的图像分类模型都是基于Transformer的。