权重初始化

权重初始化决定了训练开始时信号在网络中的传播状态。初始化太小，前向激活会一层层变得接近 0，反向梯度也可能随之消失；初始化太大，激活和梯度又可能迅速爆炸。深层网络的困难在于这种影响会被层数不断放大，所以初始化不是随便给一组小随机数，而是要尽量让每一层的输出方差保持稳定。

初始化大小选择

初始化权重的示例：

1
2
3
4
5
6
7
8
dims = [4096] * 7
hs = []
x = np.random.randn(16, dims[0])  # 16个样本，每个样本4096维

for Din, Dout in zip(dims[:-1], dims[1:]):
    W = p * np.random.randn(Din, Dout)  # p控制初始化标准差
    x = np.maximum(0, x.dot(W))         # ReLU会截断负半轴
    hs.append(x)                        # 记录每层激活，用于观察均值/方差变化

在这段代码中，使用 p 来控制权重的初始化范围。不同的 p 值会影响网络的训练效果。p 较小时（如 0.01），随着层数加深，方差逐渐趋近于 0，导致梯度消失；

p 较大时（如 0.05），方差会变得非常大，导致梯度爆炸。

Kaiming/MSRA Initialization

为了解决 p 的选择问题，使用 Kaiming/MSRA 初始化方法：

1
2
3
4
for Din, Dout in zip(dims[:-1], dims[1:]):
    W = np.random.randn(Din, Dout) * np.sqrt(2.0 / Din)  # ReLU对应的He/Kaiming初始化
    x = np.maximum(0, x.dot(W))
    hs.append(x)

这种初始化方法根据输入维度动态调整权重的标准差，从而保持每层输出的方差稳定，避免梯度消失或爆炸问题。理解这种方法的关键在于，由于每次使用 ReLU 函数会关闭一半的激活值，为了保持信号的方差不变，初始化的方差应当乘 2，因此有了这个 2/n\sqrt{2 / n} 修正。

数据处理与增强

训练 CNN 时，输入数据的尺度和分布会直接影响优化难度。若不同通道或不同特征的数值范围差异很大，梯度下降会在某些方向上走得很快、在另一些方向上走得很慢，损失曲面会变得更难优化。图像归一化的目的就是把输入变成更稳定、更接近统一尺度的分布，让后续层不用先花大量容量去适应原始像素范围。

TLDR for Image Normalization

在训练神经网络时，通常会对输入图像进行归一化处理。使用以下步骤：

  1. 计算每个通道的均值和标准差。
  2. 对每个通道进行标准化处理：
1
2
3
4
eps = 1e-8  # 防止某个通道标准差极小时除零
mean = np.mean(pixel[:, :, c])  # 第c个通道的均值
std = np.std(pixel[:, :, c])    # 第c个通道的标准差
norm_pixel[:, :, c] = (pixel[:, :, c] - mean) / (std + eps)

正则化方法

在训练中，对于 y=fW(x,z)y = f_W(x, z) 可以为其增加一定的随机性（如 Dropout，随机丢弃一定的激活值）。那么在测试中，就有：y=f(x)=Ez[f(x,z)]=∫f(x,z)p(z)dzy = f(x) = E_z[f(x, z)] = \int f(x, z)p(z)dz。这意味着在测试时，模型的输出是对所有可能的随机性进行平均的结果，从而提高模型的泛化能力。

正则化的目标不是让训练集 loss 最低，而是限制模型不要过度依赖训练集中的偶然模式。Dropout、数据增强、weight decay 都是在用不同方式增加约束：要么让特征不能互相过度 co-adapt，要么让输入变化更多样，要么让参数不要长得过大。

数据增强

数据增强（Data Augmentation）是一类非常常用的正则化手段：在不改变标签语义的前提下，对输入图像做随机变换，等价于“用同一张图生成更多不同但合理的训练样本”，从而降低过拟合、提升泛化。

一个典型训练流程可以理解为：加载图像与标签（例如“cat”）→ 对图像做随机变换（augmentation）→ 输入 CNN 前向计算 → 计算 loss 并反向传播更新参数。关键点是：增强发生在输入端，训练时每次迭代都可能看到“不同版本”的同一张图。

常见做法包括：

  • 水平翻转（Horizontal Flip）：最基础、收益稳定的增强之一。
  • 随机裁剪与尺度缩放（Random crops & scales）：
  • 训练时：随机采样裁剪区域/缩放比例（让模型对位置与尺度更鲁棒）。以 ResNet 的常见配方为例：先在 L∈[256,480]L\in[256,480] 里随机选短边长度，将图像短边 resize 到 LL，再随机采样一个 224×224224\times224 的 patch。
  • 测试时增强（Test Time Augmentation, TTA）：对一组固定裁剪/翻转的预测结果做平均，以减少单次裁剪带来的方差。例如 ResNet：先把图像 resize 到 5 个尺度 {224, 256, 384, 480, 640}，每个尺度取 10 个 224×224224\times224 crop（四角+ 中心，再加翻转），最后对这些预测求平均。
  • 颜色扰动（Color Jitter）：最简单的形式是随机改变亮度与对比度（有时也包含饱和度/色相），让模型对光照变化更稳健。
  • Cutout（或随机遮挡）：训练时将图像中的随机区域置零（或置为常数），迫使模型不要过度依赖局部显著区域；测试时使用完整图像。该方法在 CIFAR 这类小数据集上效果往往更明显，在 ImageNet 等大规模数据集上相对不那么常见。

迁移学习

有时我们并没有大量带标签的数据，这种情况下仅使用少量的数据进行训练是远远不够的。这个时候就需要先使用其他相似的数据集（如 ImageNet）进行预训练——虽然相似数据集与小数据集的数据未必相同，但是通过使用大数据集的训练，可以使得神经网络有较强的特征提取和泛化能力（有点期末周刷卷子拟合的感觉了）。

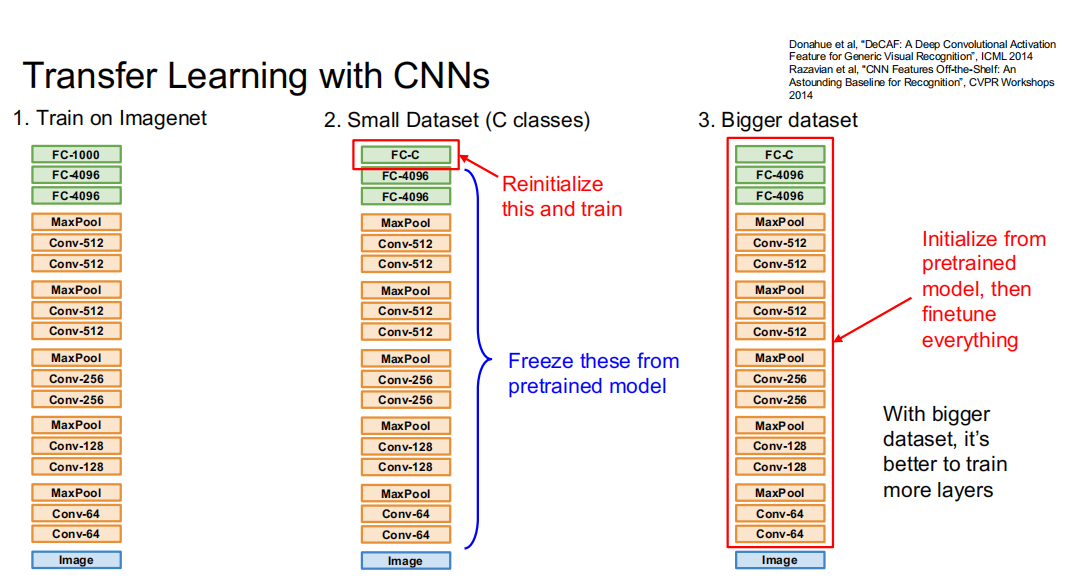
在相似数据集上训练完后，我们得到了一个具有良好特征提取能力的卷积层和全连接层。接下来要在小数据集上进行训练，以此图为例，从一个 1000 分类问题变成了一个小数据集上的 C 分类问题。此时前面的层已经有了较好的特征提取性能，使用小数据集训练未必能得到提升，因此只将最后一层 FC-1000 换成 FC-C，然后固定其他层，只用小数据训练最后一层 FC-C，就得到了一个 C 分类的神经网络。当然，如果有较大的数据集，也完全可以直接训练整个网络，提高模型在特定数据集上的表现。

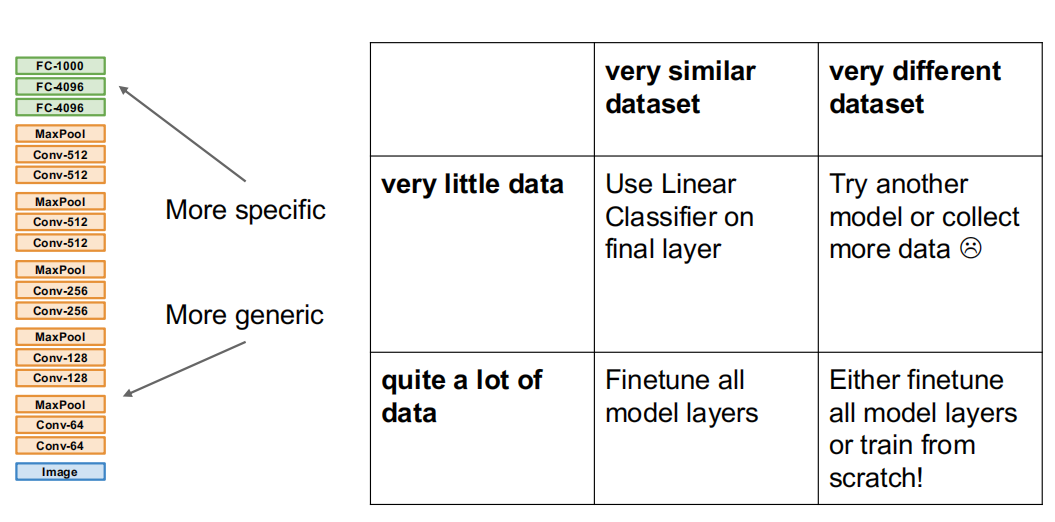
如果本来就有较大的数据集，那么完全可以直接训练所有层或从头开始训练模型；数据集较小的情况下，借助相似的数据集也可以进行迁移学习来得到需要的模型。最坏的情况是数据量小的情况下又没有相似的数据集——这种情况下模型的特征提取能力无法迁移，自然使用迁移学习也是没有意义的，只能收集更多的数据或者更换模型。

超参数选择

超参数不会通过反向传播自动学出来，却会强烈影响训练结果，例如学习率、正则强度、batch size、网络宽度和训练轮数。调参时最重要的不是一次找到完美组合，而是建立一个可诊断的流程：先确认实现正确，再用短训练筛掉明显不合适的范围，最后把算力集中到少数有希望的配置上。

检查初始 loss 是否合理

随机初始化后先跑少量 iteration，看 loss 数值是否在“合理范围”。例如 softmax 分类在未学习时，loss 常接近 −log⁡(1/C)-\log(1/C)（CC 为类别数）。若 loss 极端异常（NaN/inf 或者离谱偏大/偏小），优先检查：数据/标签、损失实现、正则项、初始化、学习率是否过大。

在很小样本上过拟合（Overfit a small sample）

取极小子集（比如几十到几百张），关闭或减弱随机增强与正则（dropout / weight decay 等），目标是让训练集准确率接近 100%、loss 明显下降。如果做不到，通常说明模型/代码/优化流程存在 bug，先不要进入大规模调参。

找到能让 loss 下降的学习率（Learning Rate, LR）

  • 固定“上一步能工作的架构”，使用全部训练数据，使用小的 weight decay（防止完全无约束），尝试一个学习率让 loss 在约 ~100 次迭代内有显著下降。
  • 常见可试的数量级：1e-1, 1e-2, 1e-3, 1e-4, 1e-5。
  • 经验信号：
  • loss 立刻爆炸/NaN：LR 可能过大（或数值不稳定）。
  • loss 几乎不动：LR 可能过小（或正则过强/梯度过小）。

粗粒度网格（或随机）搜索超参数，短训 1–5 个 epoch

在已“能下降”的 LR 附近，配合 batch size、weight decay、动量/Adam 参数、模型宽度/深度等做粗搜索。只训练很短时间（约 1–5 epoch）用于快速排序候选配置，避免把算力浪费在明显不行的组合上。

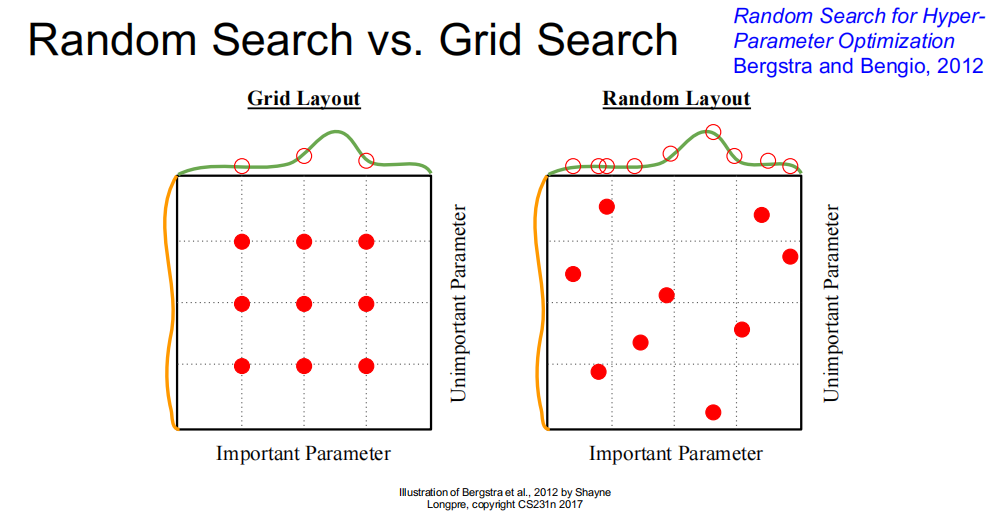
  • 当只有少数超参数真正“关键”时，随机搜索往往比网格搜索更高效：随机采样更容易覆盖到关键维度的有效取值。
  • 实操中常对 LR、weight decay 用 log 级别采样（例如在 [10−5,10−1][10^{-5}, 10^{-1}] 的 log 空间均匀采样），通常比线性步进更合理。

缩小范围，细化搜索，并训练更久

选出前几组，缩小搜索区间（例如在 log 空间里更密集采样），把训练 epoch 拉长，比较稳定收敛后的效果。

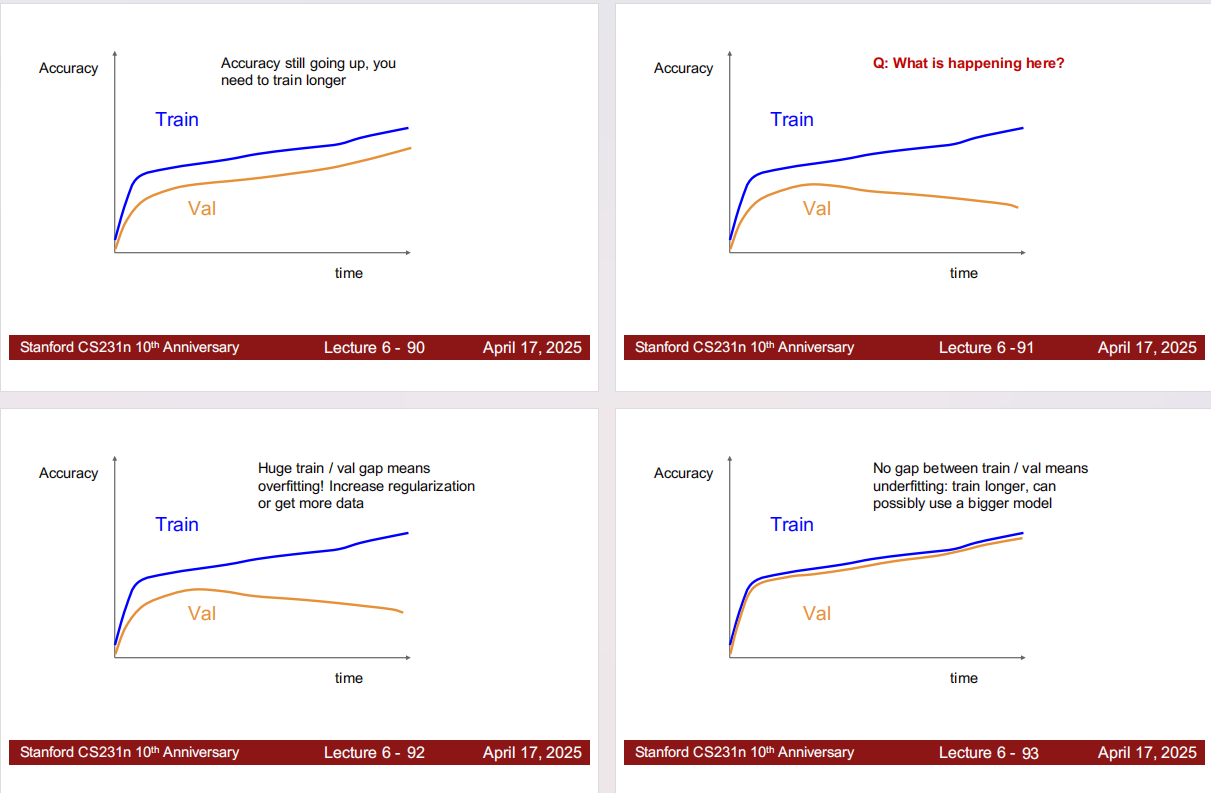
这一阶段要避免只看短训成绩，因为有些配置前期下降快但后期泛化差，有些配置前期慢但最终更稳。更长训练可以暴露学习率调度、正则强度和模型容量之间的真实关系。

结合 loss/accuracy 曲线诊断问题

只看最终一个点不够，曲线形状能直接提示下一步应该改什么。

  • 训练准确率还在上升（Train 还没饱和）：通常说明还没训练够，优先“训练更久/调整学习率调度”，再谈其它超参。
  • 训练/验证差距巨大（Train 高、Val 低）= 过拟合：增大正则（weight decay、dropout、数据增强）、降低模型容量，或获取更多数据。
  • 训练/验证都不高且差距不大（几乎无 gap）= 欠拟合：训练更久、减弱正则、或使用更大的模型。

继续细化搜索与迭代

超参数选择本质上是一个逐步缩小不确定性的调试流程，而不是一次性把所有组合都跑完。先确认代码和 loss 合理，再确认模型能在小数据上过拟合，最后才值得投入算力做大范围搜索。每一次回到 Step 5，都应该带着前一轮曲线提供的信息调整搜索范围：学习率是否还偏大、正则是否过强、模型容量是否不足、训练时间是否太短。