CS231n笔记09:循环神经网络
P1:循环神经网络
组成
循环神经网络一般用于处理序列数据,如文本和语音等。它的输入和输出的序列长度可以是任意的。循环神经网络通过中间隐藏层的循环连接来捕捉此前序列中的信息,并应用于当前的输出。
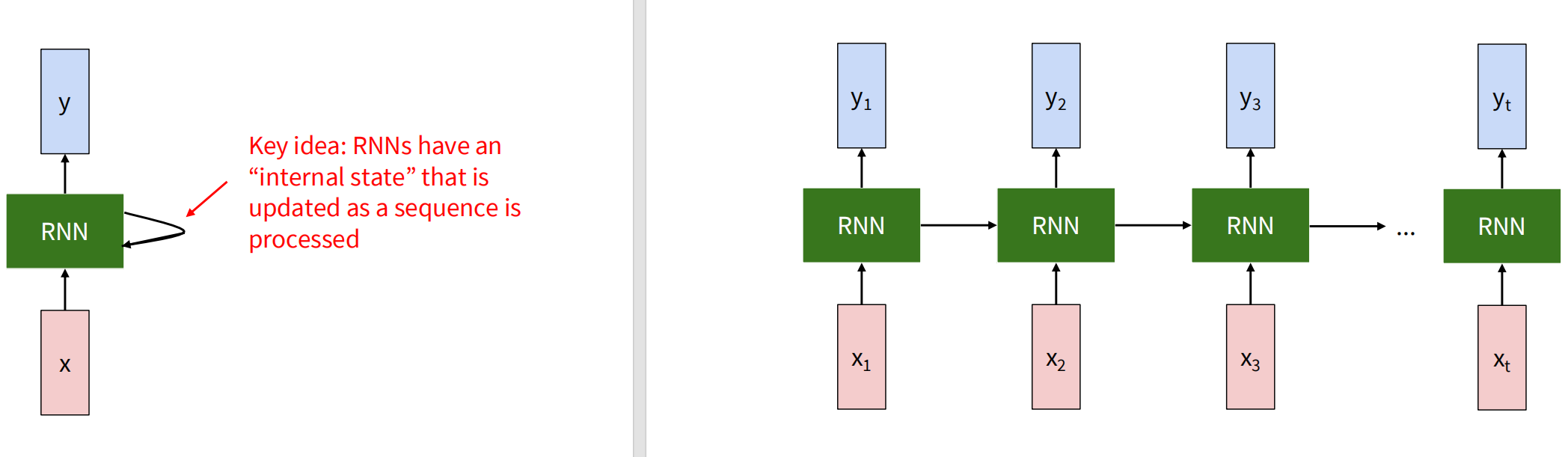
左侧是循环神经网络的单元,中间的隐藏状态随着序列处理更新,可以展开成类似右侧的形式。隐藏状态通过 来更新,其中 是变换的参数;输出则通过当前时间步的隐藏状态得到,即 得到。每个时间步使用变换的参数如 和 在序列处理的各个时间步都是共享的。
计算隐藏层时还要用到激活函数,这里使用 函数:
右图中的结构可以产生很多变种。这个结构原始的输入和输出是多对多的。如果想要将其改成多对一,可以将全部的输出经过变换产生一个最终输出,也可以直接使用最后一个时间步的隐藏状态来产生输出,因为这个隐藏状态已经包含了此前所有时间步的信息。也可以使用一对多的结构,将后续输入全部置零或者将本时间步的输出作为下一时间步的输入。
损失与反向传播
循环神经网络的损失函数可以定义为各个时间步的损失之和。当我们处理一个长序列时,在整个网络中进行反向传播会导致梯度消失或梯度爆炸,还可能会带来存储压力。为了解决这个问题,可以使用截断的反向传播(truncated backpropagation through time),即只在一定数量的时间步内进行反向传播,而不是在整个序列上进行。
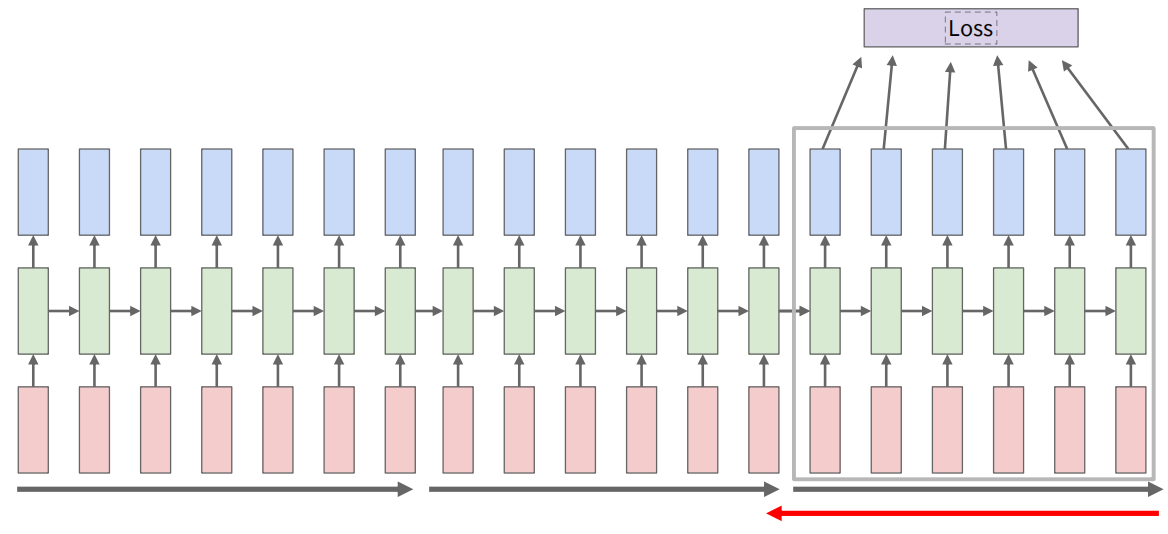
如果最终输出只有一个呢?只在最后一个截断的单元计算有效函数并进行反向传播即可。最终计算图如下:
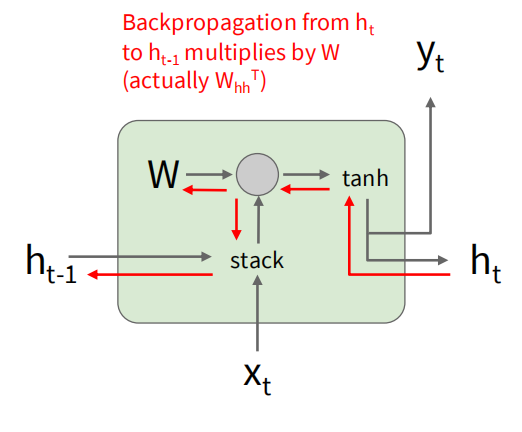
尝试推导反向传播的过程:
在每一步,有 ,其中 是每个时间步的损失函数。每一个时间步贡献的梯度是独立的,根据之前推导的矩阵乘的反向传播公式,可以得到对 的梯度为:
那么同理有:
对于隐藏状态 的梯度,需要考虑当前时间步的输出以及后续时间步的影响。当前时间步的输出对 的梯度为:
对任意时间步有
逐步展开可以得到:
可以看到,随着时间步的增加,梯度会被 反复乘积,这可能导致梯度消失或爆炸的问题。
上面的例子是使用原始公式中的矩阵运算的,实际上可以将原来的计算简化成一次矩阵乘的形式,将 和 放在一行上,将 和 放在一列上,这样计算公式简化为:
这样计算公式就只有一个参数矩阵 了。
P2:RNN应用
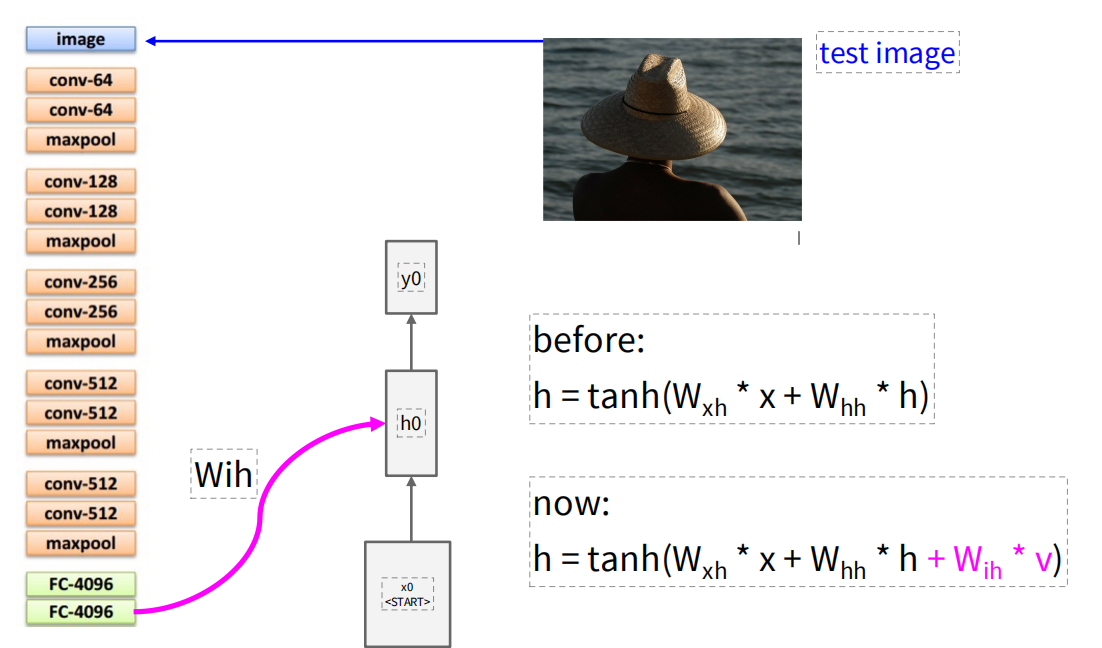
使用RNN进行图像描述时,先使用卷积神经网络将图像编码成一个定长的向量,然后将这个向量作为循环神经网络的输入来生成描述文本。不过计算隐藏状态的方法发生了改变,增加了一个矩阵 来处理将图像输入加到隐藏状态的计算中。后续的传播就是将每一个时间步的输出作为下一时间步的输入重复,直到生成结束token。
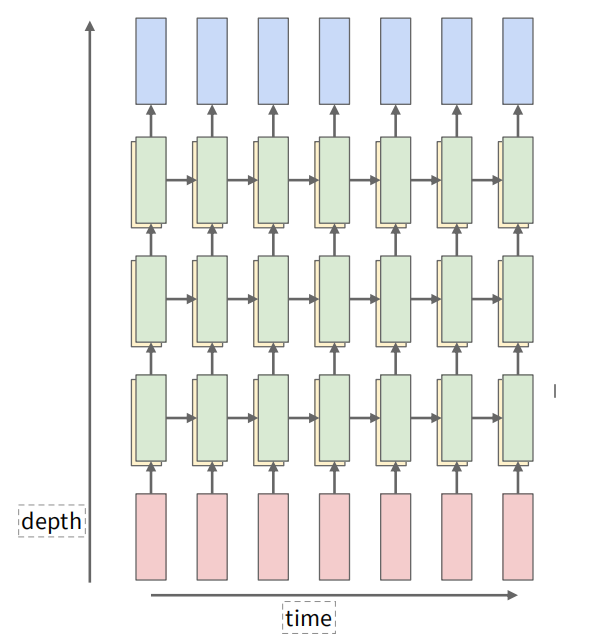
可以增加中间隐藏层的层数来提升模型的表达能力,这样每个时间步的计算就变成了多层的前向传播。对于每一层的隐藏状态计算,输入是上一层的隐藏状态和当前时间步的输入。这一部分课上似乎没有深究。
P3:Long Short-Term Memory (LSTM)
我看不懂,但我大受震撼
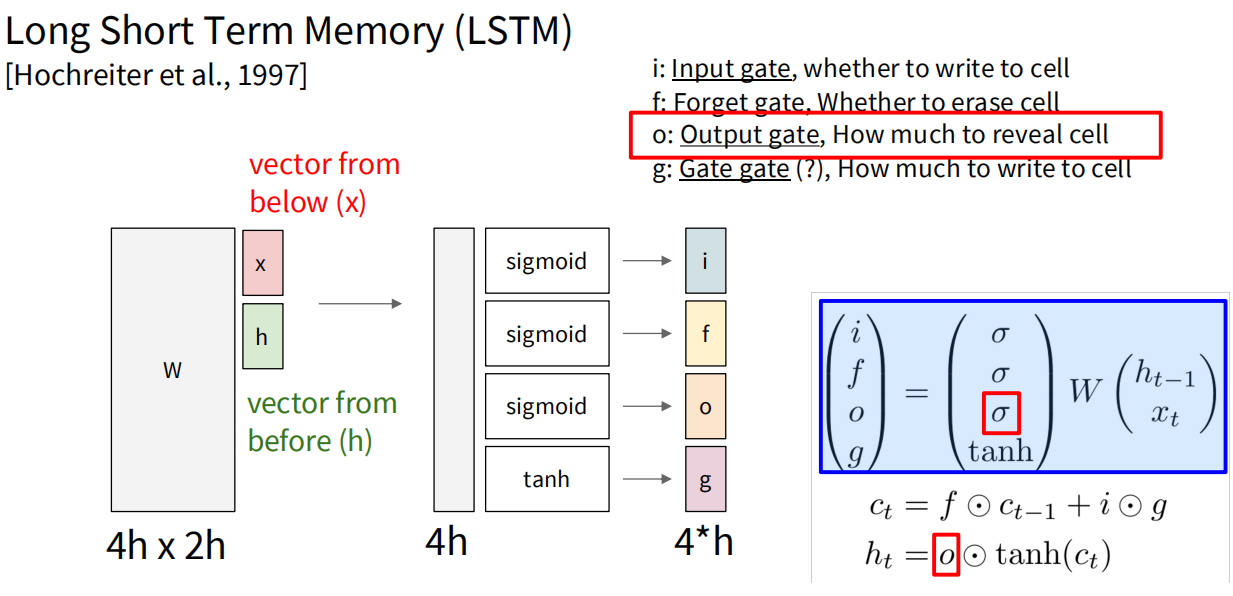
长短期记忆网络引入一个记忆元(memory cell),是一种特殊的隐状态,在网络中作为一条独立传递信息的通道。输入门i控制何时写入cell,遗忘门f控制何时重置cell,输出门o控制从cell读取输出信息,(Gate gate是什么鬼)门g则控制写入cell的信息。W将上一时间步的隐藏状态和输入组成的向量变换成四个通道的值,并经过对i,f,o门的sigmoid处理和对g门的tanh处理得到相应的门控值。cell状态通过遗忘门和输入门的控制进行更新,最终输出由输出门控制。
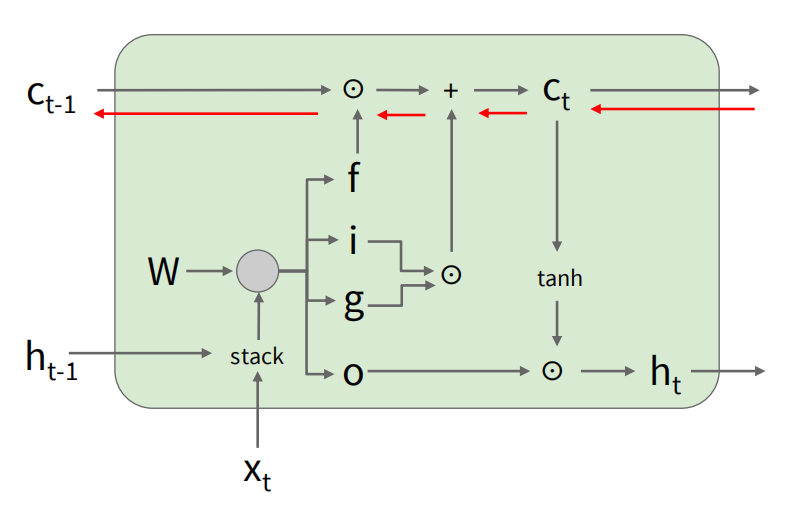
现在,i,f,o三个门的值都被压缩到了0到1之间,且大小与输入一致,这样就可以通过门控机制来控制信息的流动。对于记忆元内容的更新,有:
其中 表示元素级乘法。遗忘门 控制了之前的记忆元内容 的保留程度,而输入门 和门 控制了新信息的写入程度。输出门 则控制了最终输出的生成:
f = 1,i = 0时,cell状态完全保留之前的内容;f = 0,i = 1时,cell状态完全被新的信息覆盖。通过调整这些门的值,LSTM能够灵活地保留或更新信息,从而更好地捕捉长期依赖关系,缓解RNN中的梯度消失问题。有一个缺点是计算复杂度变高了,权重矩阵的学习成本更高了。









